Понятие о сложной функции

Определение 1: Если на множестве Х определена функция Z = φ(х) со множеством значений Z, а на множестве Z – функция y = f(z), то функция y = f [φ (x)] называется сложной функцией от х (композицией или суперпозицией).

 

Правило дифференцирования сложной функции:

ТП: Если функция х = φ(t) имеет производную в точке t₀, а функция y = f(х) имеет производную в соответствующей точке х₀ = φ(t₀), то сложная функция f [φ (t)] имеет производную в точке t_{0 ,} которую можно вычислить по формуле:

y'(t₀) = f ' (x₀) · φ' (t₀)

Формулы дифференцирования сложной функции:

I. (Ln 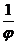φ')' = · φ'

II. (Log_a 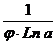φ)' = · φ'

III. (φⁿ)' = n · φ^n-1 · φ''

IV. (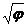)' = 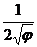· φ'

V. (a^φ)' =a^φ · Ln a· φ'

VI. (e^φ)' = e^φ · φ'

VII. (sin φ)' =cos φ · φ'

VIII. (cosφ)' = - sinφ · φ'

IX. (tg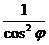φ)' = · φ'

X. (сtg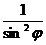φ)' = · φ'

XI. (arcsin 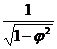φ)' = · φ'

XII. (arccos 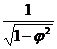φ)' = - · φ'

XIII. (arctg 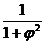φ)' = · φ'

XIV. (arcctg 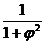φ)' = - · φ'

Например:

1. (sin 5x)^' = cos 5x ·(5x) ^' = cos 5x · (5) = 5 cos 5x (VII)

2. (3tg(x + 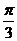))' = 3 ·(tg(x + 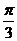))' = 3 · 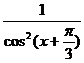' · (x + 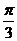)' = 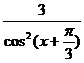· [(x)' + 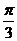'] = 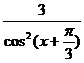· (1 + 0) = 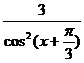(IX)

3. y = e^{arctg x}

y' = (e^{arctg x})' = e^{arctg x} · (arctg x)' = e^{arctg x} · =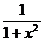

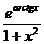
4. ((5x -3)¹⁰)' = 10 · (5x - 3) · (5x -3)' = 10 · (5x - 3) · [(5x) ' – (3)'] = 10 · (5x - 3) · (5 - 0) = 10 · 5 · (5x - 3) = 50(5x - 3)

Другие примеры вычисления производной:

1. 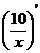= (10 · х^-1) = 10 · (-1) · х^-1-1 = - 10 ·х^-2 = - 10 · х² = - 10 · =

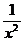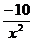
2. = (3 · x^-9)' = 3 ·(-9) · x^-9-1 = -27x^-10 = -27 · =

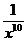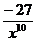
3. 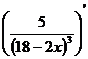= (5·(18 – 2x)^-3)' = 5((18 – 2x)^-3)' = 5 · (-3) · (18 – 2x)^-3-1 · (2x)' = -15·(18 – 2x)^-4 ·2 = -30 · =

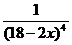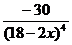
4. ()' = ()' = = = =

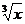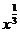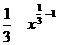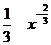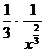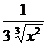
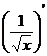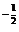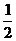5. = (x 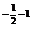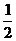)' = - · x = - · x = - = - =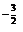

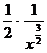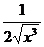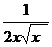
6. cos² (3x - 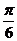) = cos^2-1 (3x - 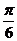) · cos^2-1 (3x - 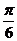)' = 2cos (3x - 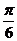) · (-sin (3x - 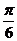)) ·(3x - 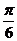)' = - 2cos (3x - 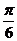) · sin (3x - 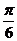) · ((3x) ' –(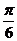)') = - 2 · cos (3x - 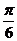) · sin (3x - 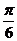) · 3 = - 6 · cos (3x - 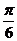) · sin (3x - )

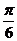Задание 2.

Вычислить производные:

2.01 а). y = 6x² + 18x + 7

б). y =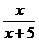

в). y = (x³ - 1)¹⁰⁰

 

2.02 а). y = 3cos – x⁶ + 5tg x

б). y = (1 + 4x³) · sin x

в). y = e ^{4x - 3}

2.03 а). y = 4x⁵ - 3sin x + 5tg x

б). y = x² · tg x

в). y = a ^3x

 

2.04 а). y = 4cos x – 5tg x + 3

б). y = sin² x

в). y =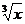

 

2.05 а). y = 5ln x - 7cos x – x⁴

б). y =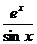

в). y = sin(x² + 5x)

 

2.06 а). y = 15 + x³ + 3x² + sin x

б). y = x² · ctg x

в). y = cos¹⁰⁰x

2.07 а). y = 2x² – 4x + 3

б). y = e ^tg x

в). y =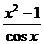

 

2.08 а). y = 4 – 2sin x + 2x¹²

б). y = (x + 5) · cos x

в). y = (3x + x²)¹⁰

 

2.09 а). y = 25x²+ 6 x – ctg x

б). y =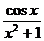

в). y = e ^{sin x}

2.10 а). y = 3 x + 9 x² + 2

б). y = x³ · tg x

в). y = arcsin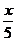

Пример построения уравнения касательной.

Найти уравнение касательной к кривой y = 4x² + 4x – 3, в точке, абсцисса которой равна – 3.

Решение:

Уравнение касательной в общем виде:

y_к = y'(x₀) · (x – x₀) + y(x₀)

y'(x) = (4x² + 4x - 3)' = 8x + 4

y'(x₀) = y'(-3) = 8 · (-3) + 4 = -24 + 4 = -20

y(x₀) = y(-3) = 4·(-3)² + 4·(-3) – 3 = 4 · 9 – 12 – 3 = 21

y_к = -20·(x –(-3) + 21) = -20·(x + 3 + 21= -20x – 60 + 21 = -20x – 39

Ответ: y_к = -20x – 39.