y = 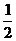 (x4 – 6x2 + 5)
(x4 – 6x2 + 5)
Решение:
1. Данная функция является рациональной, она определена, непрерывна и дифференцируема на множестве всех действительных чисел.
2. Определим четность:
y(-x) = 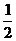 ((-x)4 - 6·(-x)2 + 5) =
((-x)4 - 6·(-x)2 + 5) = 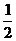 (x4 - 6x2+ 5),
(x4 - 6x2+ 5),
y(-x) = y(x), следовательно данная функция является четной и ее график симметричен относительно оси ординат.
3. Определим точки пересечения графика функции с осями координат:
а). Для того чтобы найти точки пересечения графика с осью абсцисс, решим
уравнение у = 0:
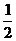 (x4 – 6x2 + 5) = 0,
(x4 – 6x2 + 5) = 0,
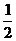 x4 –
x4 – 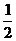 ·6·x2 +
·6·x2 +  = 0,
= 0,
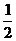 x4 - 3x2 +
x4 - 3x2 +  = 0, решим это биквадратное уравнение, сделав замену z = x2:
= 0, решим это биквадратное уравнение, сделав замену z = x2:
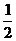 z2 – 3z +
z2 – 3z +  = 0,
= 0,
Д = (-3)2 – 4 · 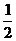 ·
·  = 9 -5 = 4,
= 9 -5 = 4,
z1 =  = 5, z2 =
= 5, z2 = 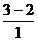 = 1,
= 1,
Делаем обратную замену:
x2 = 5,
x2 =  ,
,
x2 = -  ,
,
x2 = 1,
x3 = 1,
x4 = 4. Точки пересечения графика с осью абсцисс: ( ;0), (-
;0), (-  ;0), (1;0), (-1;0)
;0), (1;0), (-1;0)
б). Пересечение графика с осью ординат определяем, вычислив значение у(0):
у(0) = 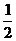 (0 – 6 · 0 + 5) =
(0 – 6 · 0 + 5) =  ,
,
Точка пересечения графика с осью ординат:
(0;  ).
).
4. Для нахождения точек возможного экстремума, вычислим первую производную:
y' = [ 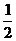 (x4 – 6x2 + 5)]' = (
(x4 – 6x2 + 5)]' = ( - 3x2 +
- 3x2 +  )' =
)' = 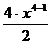 - 3 · 2 · x2-1 + 0 = 2x3 – 6x,
- 3 · 2 · x2-1 + 0 = 2x3 – 6x,
затем решал уравнение у' = 0, получим абсциссы точек возможного экстремума:
2x3 – 6x = 0,
2x(x2 - 3) = 0,
2x = 0 или x2 – 3 = 0,
x1 = 0 x2 = 3,
x2 = 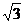 ,
,
x2 = - 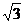 .
.
На вспомогательном чертеже исследуем знаки производной:
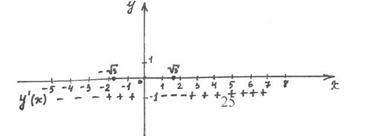
y'(-3) = 2·(-3)3 - 6·(-3) = -54 + 18 < 0
y'(-1) = 2·(-1)3 - 6·(-1) = -2 + 6 > 0
y'(1) = 2·13 - 6·1 = 2 - 4 < 0
y'(3) = 2·33 - 6·3 = 54 – 16 > 0
Т.к. при переходе через точку с абсциссой (- 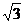 ) производная меняет знак с «-» на «+», то это абсцисса точки минимума.
) производная меняет знак с «-» на «+», то это абсцисса точки минимума.
При переходе через точкус абсциссой (0) производная меняет свой знак с «+» на «-», следовательно, это абсцисса точки максимума.
При переходе через точкус абсциссой 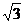 производная меняет свой знак с «-» на «+», следовательно это абсцисса точки минимума.
производная меняет свой знак с «-» на «+», следовательно это абсцисса точки минимума.
Определим координаты точек экстремума, для этого вычислим значение функции в полученных значениях х:
y (- 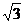 ) =
) = 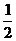 ((-
((- 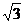 )4 – 6 · (-
)4 – 6 · (- 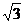 )2 + 5) =
)2 + 5) = 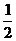 (9 – 6 · 3 + 5) = -2,
(9 – 6 · 3 + 5) = -2,
y (0) =  ,
,
y (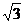 ) =
) = 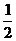 ((
((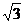 )4 – 6 · (
)4 – 6 · (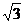 )2 + 5) = -2/
)2 + 5) = -2/
Вывод: Функция убывает на промежутке (- ∞; - 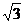 ) и на (0;
) и на (0; 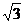 )
)
Функция возрастает на промежутке (- 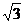 ; 0) и на (
; 0) и на (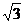 ;∞)
;∞)
Минимумы функции:
при х = - 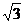 , у (-
, у (- 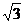 ) = -2 и
) = -2 и
при х = 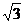 , у (
, у (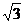 ) = -2.
) = -2.
Максимум функции:
при х = 0, у (0)=  .
.
5. Найдем значения х, при которых имеет точки перегиба, для этого найдем вторую производную: у'' = (2х3 – 6х)' = 6х2 – 6 и решим уравнение:
6х2 – 6 = 0,
6(х2 - 1) = 0,
х2 – 1 = 0,
х1 = 1,
х2 = -1.
Пользуясь вспомогательным чертежом определим точки перегиба:

у''(-2) = 6((-2)2 - 1) = 6 · (4 - 1) > 0
у''(0) =6 · (0 - 1) < 0
у''(2) = 6(22 - 1) = 6 · (4 - 1) > 0
Т.к. при переходе через значение х = -1, х = 1, вторая производная меняет свой знак, то график функции имеет точку перегиба при рассматриваемых значениях х, причем на промежутках (- ∞; -1) и (1;∞) направления выпуклости графика вниз, а на промежутке (-1; 1) – вогнут книзу.
6. Пользуясь полученными данными строим график:
 |
Задание 5.
Построить графики функций:
5.01 у = 1+ 6х – 3х3
5.02 у = х3- 3х2 + 7
5.03 у = х4+ 4х - 6
5.04 у = х3- 3х + 2
5.05 у = 2 - х – х3
5.06 у = 2х3+ х2 - 2
5.07 у = 3х4+ 2х2 - 5
5.08 у = х3 + 4х
5.09 у = х4 - 2х3 – 2х2
5.10 у = 3+ 8х – х2
 2018-01-08
2018-01-08 439
439







