2.1 Предел функции в точке
Определение 1. (на языке бесконечно малых и бесконечно больших функций)
Число A называется пределом функции f(x) при x→a, если функция f(x) в точке a представима в виде
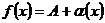 , где α(х) – бесконечно малая функция при x→a.
, где α(х) – бесконечно малая функция при x→a.
Запись: 

Определение 2. (на языке ε, δ)
Число A называется пределом функции f(x) в точке а, если для любого положительного числа ε существует такое положительное число δ, что для всех  выполняется неравенство
выполняется неравенство 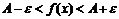 .
.
 Пояснение (см. рис.): смысл определения в том, что для достаточно близких к а значениях аргумента x соответствующие значения функции отличаются от значения A сколь угодно мало.
Пояснение (см. рис.): смысл определения в том, что для достаточно близких к а значениях аргумента x соответствующие значения функции отличаются от значения A сколь угодно мало.
Примеры:
1) 
2)  , но при x=a 3)
, но при x=a 3)  , но f(a) = 2
, но f(a) = 2
функция не определена
2.2. Односторонние пределы
Рассмотрим график некоторой функции y=f(x):

При x→a – (слева)  левосторонний предел
левосторонний предел
При x→a + (справа)  правосторонний предел
правосторонний предел
Но при этом  не существует!
не существует!
Таким образом, предел функции в точке существует, если существуют и равны оба односторонних предела.
2.3. Непрерывность функции в точке
Определение. Функция f(x) называется непрерывной в точке а, если предел функции при x→a равен значению функции в точке а. 
Этому определению можно дать несколько трактовок, одна из которых:
Функция непрерывна в точке а – значит 
Если функция непрерывна в каждой точке некоторого промежутка, то она непрерывна на всем промежутке; если функция непрерывна в каждой точке области определения, то она непрерывна на всей области определения функции. Непрерывность функции – очень важное свойство. При изучении программы средней школы мы работаем только с непрерывными на своей области определения функциями.
2.4. Виды разрывов
1.  Устранимый разрыв, разрыв нулевого рода – существуют и равны односторонние пределы, и функция определена в точке.
Устранимый разрыв, разрыв нулевого рода – существуют и равны односторонние пределы, и функция определена в точке.
Пример:  Здесь:
Здесь: 
2. Разрыв первого рода – «скачок» - существуют оба односторонних предела, нет общего.

Пример:  Здесь:
Здесь:  не
не
существует.
3.  Разрыв второго рода - не существует односторонних пределов или хотя бы одного из них (гипербола)
Разрыв второго рода - не существует односторонних пределов или хотя бы одного из них (гипербола)
Пример:  . Здесь: в точке 0 предел слева равен −∞, предел справа +∞.
. Здесь: в точке 0 предел слева равен −∞, предел справа +∞.
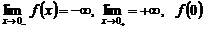 не существует.
не существует.
2.5. Свойства непрерывных функций
Теорема 1. (первая теорема Больцано-Коши)
Если функция f(x) непрерывна на отрезке [a, b], причем значения функции в точках a и b разных знаков (f(a)∙f(b)<0), то существует такая точка cÎ[a, b], что f(c) = 0.
Графически: на отрезке [a, b] есть точка, в которой график функции пересекает ось Х.

Теорема 2. (вторая теорема Больцано-Коши)
Непрерывная на отрезке функция вместе с любыми двумя значениями принимает и все промежуточные значения.
Т.е. для любого С Î [f(a), f(b)] существует точка c такая, что f(c) = C
Теорема 3. (вторая теорема Вейерштрассе)
Непрерывная на отрезке функция достигает на нем наименьшего и наибольшего значений.
 Например, функция f(x) = {x} – мантисса числа (дробная часть)
Например, функция f(x) = {x} – мантисса числа (дробная часть)
На отрезке [0, 2] функция не имеет наибольшего значения, значит, функция разрывная (разрыв 1 рода).
2.6. Асимптоты графика функции
1. Вертикальные. Прямая x = a является вертикальной асимптотой графика функции, если
 т.е. не существует.
т.е. не существует.
Пример:
1)  здесь x = -2 вертикальная асимптота,
здесь x = -2 вертикальная асимптота, 
2)  x = ±1 – вертикальные асимптоты,
x = ±1 – вертикальные асимптоты, 
3)  x = -1 - вертикальная асимптота,
x = -1 - вертикальная асимптота, 
4)  - множество вертикальных асимптот графика;
- множество вертикальных асимптот графика;
5) 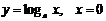 - вертикальная асимптота,
- вертикальная асимптота, 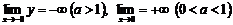
 2018-01-08
2018-01-08 2900
2900
