2.1. Степенная функция 
Свойства функции и вид графика зависят от показателя степени n.. При этом графики всех степенных функций проходят через точку с координатами (1; 1).
Вид графика:
| 1. Натуральный показатель | |
 Для четного показателя: функция Четная; Ограниченная снизу; имеет экстремум – минимум в точке x=0 Для четного показателя: функция Четная; Ограниченная снизу; имеет экстремум – минимум в точке x=0 |  Для нечетного показателя: функция Нечетная; Неограниченная; Монотонно возрастающая; экстремумов не имеет, x=0 – точка перегиба Для нечетного показателя: функция Нечетная; Неограниченная; Монотонно возрастающая; экстремумов не имеет, x=0 – точка перегиба |
| 2. Целый отрицательный показатель | |
Для четного показателя: функция четная; экстремумов не имеет; ограниченная снизу Ось Ox – горизонтальная асимптота;  Ось Oy – вертикальная Ось Oy – вертикальная |  Для нечетного показателя: функция – нечетная; неограниченная; монотонно убывающая; Ось Ox – горизонтальная асимптота; Ось Oy – вертикальная Для нечетного показателя: функция – нечетная; неограниченная; монотонно убывающая; Ось Ox – горизонтальная асимптота; Ось Oy – вертикальная |
| 3. Рациональный показатель (дробный) | |
 Для положительного показателя: функция общего вида, монотонно возрастает, экстремумов и асимптот не имеет Для положительного показателя: функция общего вида, монотонно возрастает, экстремумов и асимптот не имеет |  Для отрицательного показателя: функция общего вида; монотонно убывает Для отрицательного показателя: функция общего вида; монотонно убывает |
2.2. Рациональная функция (частные случаи)
· Линейная функция. Общий вид  . Графиком функции является прямая. Число k – угловой коэффициент
. Графиком функции является прямая. Число k – угловой коэффициент 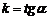 . Если k>0 линейная функция возрастает, k<0 - убывает, k=0 – прямая параллельна оси абсцисс (в этом случае имеем частный случай – постоянную функцию, которая в общем виде задается уравнением y = C).
. Если k>0 линейная функция возрастает, k<0 - убывает, k=0 – прямая параллельна оси абсцисс (в этом случае имеем частный случай – постоянную функцию, которая в общем виде задается уравнением y = C).
· Квадратичная функция. Общий вид  . Графиком функции является парабола. Число
. Графиком функции является парабола. Число  – старший коэффициент. Отвечает за направление ветвей параболы; при a>0 – ветви вверх, при a<0 – ветви вниз. Коэффициент b отвечает за вершину параболы; координаты вершины:
– старший коэффициент. Отвечает за направление ветвей параболы; при a>0 – ветви вверх, при a<0 – ветви вниз. Коэффициент b отвечает за вершину параболы; координаты вершины:  ; прямая
; прямая 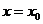 - ось симметрии параболы. Нули функции – это корни квадратного уравнения
- ось симметрии параболы. Нули функции – это корни квадратного уравнения  .
.
На самом деле график любой квадратичной функции можно получить из графика функции 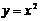 путем преобразования.
путем преобразования.
Например:  ;
;
Графиком функции является парабола, ветви вверх, вершина (2,5; -0,25), ось симметрии 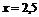 , нули функции
, нули функции  .
.
2.3. Показательная и логарифмическая функции
Функции  являются взаимно обратными функциями; их графики симметричны относительно прямой y = x.
являются взаимно обратными функциями; их графики симметричны относительно прямой y = x.
Для функции  ; для функции
; для функции  .
.
Обе функции существуют для основания  .
.
Если основание:
·  , то показательная и логарифмическая функции монотонно возрастают;
, то показательная и логарифмическая функции монотонно возрастают;
·  , то показательная и логарифмическая функции монотонно убывают.
, то показательная и логарифмическая функции монотонно убывают.
Вид графика экспонента


Для показательной функции характерная точка (0, 1), для логарифмической (1,0);
Для показательной функции ось абсцисс – горизонтальная асимптота, для логарифмической функции ось ординат – вертикальная асимптота.
.
2.4. Тригонометрические функции
· Функция 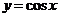 :
: 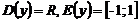 , четная, период
, четная, период  , ограниченная, имеет экстремумы (максимумы и минимумы), асимптот нет, график – косинусоида.
, ограниченная, имеет экстремумы (максимумы и минимумы), асимптот нет, график – косинусоида.

· Функция  :
: 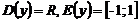 , нечетная, период
, нечетная, период  , ограниченная, имеет экстремумы (максимумы и минимумы), асимптот нет, график – синусоида.
, ограниченная, имеет экстремумы (максимумы и минимумы), асимптот нет, график – синусоида.

· Функция  :
:  , нечетная, период
, нечетная, период  , возрастает на каждом периоде, экстремумов не имеет, прямые
, возрастает на каждом периоде, экстремумов не имеет, прямые  - вертикальные асимптоты, график – тангенсоида
- вертикальные асимптоты, график – тангенсоида
·  Функция
Функция  :
:  , нечетная, период
, нечетная, период  , убывает на каждом периоде, экстремумов не имеет, прямые
, убывает на каждом периоде, экстремумов не имеет, прямые 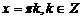 - вертикальные асимптоты, график –котангенсоида.
- вертикальные асимптоты, график –котангенсоида.

- Обратные тригонометрические функции
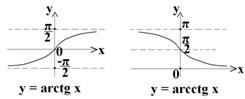

Обратна y=sinx Обратна y=cosx Обратна y=tgx Обратна y=ctgx
на: [−π/2, π/2] на [0, π] на (−π/2, π/2) на (0, π)
Для функции  - горизонтальные асимптоты; для функции
- горизонтальные асимптоты; для функции 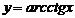 -
- 
 2018-01-08
2018-01-08 1703
1703
