Домашнее задание № 5 «Вычисление пределов»

Часть 1.

1) -42; 2) -3; 3) 5; 4) -7; 5) 49; 6) 0; 7) ; 8) ; 9) 2; 10) 1; 11) ; 12) ; 13) 0; 14) ∞; 15) .

Часть 2.

Лекция 4. Замечательные пределы

4.1. Эквивалентные Б.М.Ф. и Б.Б.Ф.

Эквивалентные бесконечно малые и бесконечно большие функции – это функции одного порядка, т.е.

, где α(x), β(x) – б.м.ф. и Φ(x), G(x) – б.б.ф.

Цепочка эквивалентных бесконечно малых функций (α(x)→0):

α(x) ~ sinα(x) ~ tgα(x) ~ arcsin α(x) ~ arctg α(x) ~ ln(1+α(x)) ~ e ^α(x) – 1

Теорема. Предел отношения б.м.ф. (или б.б.ф.) равен пределу отношения их эквивалентных.

4.2. Замечательные пределы

Первый замечательный предел:

Следствия:

Второй замечательный предел:

Примеры: 1) 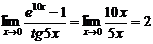, т.к. при x→0 10x ~ 5x – эквивалентные б.м.ф.

Тогда: e ^10x−1 ~ 10x, tg5x ~ 5x;

2) 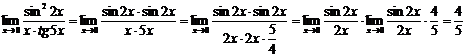; (tg5x ~ 5x);

3) ;

sin(x/2) ~ x/2, ;

4)