Лекция 2. Физический и геометрический смысл первой и второй производной

2.1. Вторая производная – это производная от производной функции; обозначается двумя штрихами т.е. .

Например, для функции .

Вторая производная для первой производной является такой же характеристикой, как первая производная для самой функции. Она характеризует характер монотонности производной и точки экстремума производной. Вторая производная помогает точнее определять поведение функции на отрезке (или на области определения). Исследование функции при помощи второй производной происходит согласно порядку, уже определенному выше. А именно, нужно искать точки, в которых вторая производная обращается в нуль или не существует. Как правило, их называют критические точки второго рода.

Обратите внимание, что для рациональных функций при нахождении последовательно первой и второй производных, степень функции понижается каждый раз на порядок. Т.е., если исследуемая функция третьей степени, то ее первая производная меняется по квадратичному закону, а вторая – по линейному.

А для тригонометрических функций синус и косинус, вторая производная фактически превращается обратно в саму функцию. Например: .

2.2. Физический смысл первой и второй производной

С точки зрения механики. Если задан закон, по которому путь (или перемещение) материальной точки зависит от переменной – времени, т.е. S (t), x(t), тогда: первая производная показывает скорость изменения перемещения, а вторая производная – скорость изменения скорости движения, т.е. ускорение.

или

Например:

Равномерное движение: (скорость постоянна, ускорение равно нулю);
Равноускоренное движение: (скорость меняется по линейному закону, ускорение постоянно)

Пример. Движение материальной точки осуществляется по закону .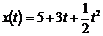

Найдите: а) начальную скорость движения v₀; б) ускорение движения a(t); в) время, через которое скорость точки станет равной 12.

Решение. а) б) в)

2.3. Геометрический смысл первой и второй производной

2.3.1. Первая производная. Значение производной в точке x₀ равно угловому коэффициенту касательной, построенной к графику соответствующей функции в точке с абсциссой x₀:

, α – угол наклона касательной к оси абсцисс.

2.3.2. Вторая производная.

«Наглядным свойством графика функции на некотором промежутке является его выпуклость. График функции может иметь выпуклость как вверх (например, у функции 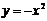), так и выпуклость вниз (например, у функции ).

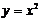Точка, в которой меняется характер выпуклости, называется точкой перегиба функции.

Простейший пример – это функция : для нее точка x=0 является точкой перегиба.

Если в этой точке провести касательную, то по одну сторону от точки перегиба график функции начинает уходить выше касательной (становится выпуклым вниз), а по другую сторону - график уходит вниз (становится выпуклым вверх).

Точки перегиба появляются в том случае, если первая производная при переходе через эту точку обратилась в нуль или не существовала, но знак не поменяла.

Например: 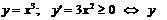монотонно возрастает. При этом вторая производная: в точке 0 меняет знак; при - выпуклость вверх, при - выпуклость вниз.

В общем виде алгоритм нахождения точек перегиба:

· Найти вторую производную функции ;

· Найти критические точки второго рода, т.е. приравнять вторую производную к нулю и решить уравнение ;

· Определить знаки второй производной на получившихся промежутках;

· По знаку второй производной сделать выводы о наличии точек перегиба: это критические точки, в которых вторая производная меняет знак;

· При этом:

Если на промежутке - график функции имеет выпуклость вниз ();

Если на промежутке - график функции имеет выпуклость вверх ()

2.4. Задачи

Найти точки перегиба функции и определить выпуклость графика:

1)

Вывод: x=0 – точка перегиба: выпуклость графика – вверх;

- выпуклость графика – вниз.

2)

Критических точек второго рода бесконечно много. Однако, учитывая, что наименьший период функции равен π, достаточно определить наличие точек перегиба на этом периоде:

Определение знаков второй производной:

Вывод: точки перегиба .

В точках - перегиб с выпуклости графика вверх на выпуклость вниз;

В точках - перегиб с выпуклости графика вниз на выпуклость вверх.