1.1. Дифференциал
Пусть функция f(x) дифференцируема в точке x0 Î(a, b), т.е. существует 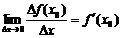 .
.
Тогда по теореме о представлении функции в виде суммы ее предела и б.м.ф. (см. раздел 3, тема 3.2.) «Предел функции в точке»: если  , то f(x) = A + α(x)) имеем:
, то f(x) = A + α(x)) имеем:

Здесь слагаемые α(x) и Δx есть бесконечно малые более высокого порядка, чем величина  . Тогда величина
. Тогда величина  составляет главную часть приращения функции в точке x0. Это и есть дифференциал.
составляет главную часть приращения функции в точке x0. Это и есть дифференциал.
Определение. Дифференциалом функции y=f(x) в точке x0 называется линейная относительно Δx величина  , составляющая главную часть приращения функции в точке x0.
, составляющая главную часть приращения функции в точке x0.
Обозначение: 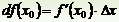
Если функция дифференцируема в каждой точке интервала (a, b), то  или
или 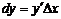
Для функции  .
.
Тогда запись: d f(x) = f / (x) dx или d y = y / dx
Т.е. дифференциал функции равен произведению производной на дифференциал аргумента.
При этом, если f / (x0) = 0, то d f(x0) = 0. Здесь f / (x0) Δx не главная часть приращения функции, т.к. 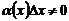 .
.
Примеры. Найти дифференциалы следующих функций:
1) 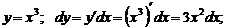
2) 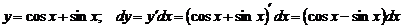
1.2. Дифференциал сложной функции
Если y = f(u), u = g(x): 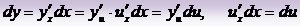
Таким образом, форма дифференциала не зависит от того, является ли аргумент независимой переменной или функцией другого аргумента. Это свойство называется инвариантность дифференциала.
Пример: 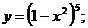
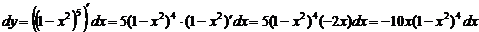
1.3. Основные свойства дифференциала: u и v -дифференцируемые функции
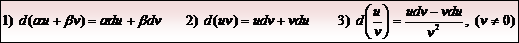
 2018-01-08
2018-01-08 569
569








