1.1. Первообразная
Определение. Функция F(x) называется первообразной функции f(x), если они обе существуют на одном и том же множестве, и производная функции F(x) равна функции f(x).
F / (x) = f (x)
Например, функция:
· y = sin x - первообразная для y = cos x
· y = - cos x - первообразная для y = sin x
· y = 2x + 1 - первообразная для y = 2
· y = ln x - первообразная для y = 1/x (на множестве x > 0) и т.д.
Операция нахождения первообразной называется интегрирование. Это операция, обратная дифференцированию.
Вспоминаем таблицу первообразных элементарных функций
| Функция f(x) | Первообразная F(x) |
| 1) Постоянная: C |  |
2) Степенная:  | 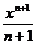 |
Частные случаи: 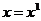 | 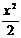 |
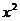 | 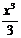 |
 | 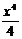 |
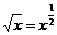 | 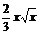 |
Для степенной 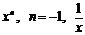 | 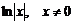 |
3) Показательная: 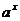 | 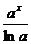 |
Частный случай:  |  |
4) Тригонометрические: 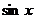 | 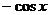 |
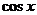 | 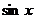 |
 |  |
 | 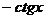 |
| 5) Правила интегрирования: | |
5.1)  | 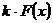 |
5.2) 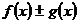 |  |
5.3) Для сложной функции 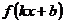 | 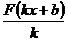 |
Для любой функции существует бесконечно много первообразных, которые имеют общую часть, а различаются лишь постоянными (числами).
Например, для функции 
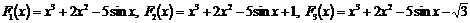 являются первообразными, т.к.
являются первообразными, т.к. 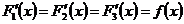 . И подобных первообразных можно составить сколько угодно.
. И подобных первообразных можно составить сколько угодно.
Определение. Совокупность всех первообразных для данной функции f(x) называется неопределенным интегралом от этой функции и обозначается 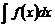 .
.
Здесь:
f(x) -- подинтегральная функция, f(x)dx – подинтегральное выражение, dx – дифференциал аргумента.
Тогда, общая формула: 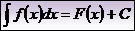 , где C – произвольная постоянная.
, где C – произвольная постоянная.
Таким образом, для вычисления неопределенного интеграла, нужно найти все первообразные
заданной функции.
Например: 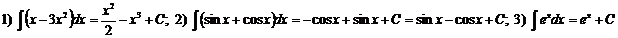 и т.д.
и т.д.

Геометрически неопределенный интеграл представляет собой семейство параллельных интегральных кривых F(x), F(x)+C1, F(x)+C2 и т.д.
Отмечаем: если функция y=f(x) непрерывна на некотором промежутке, то на этом промежутке существует первообразная функции F(x), а, следовательно, и неопределенный интеграл ∫f(x)dx.
Примеры. Найти:
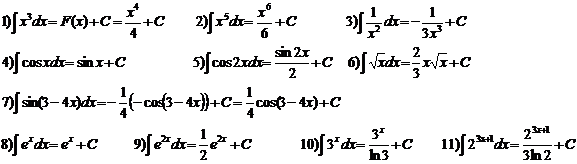
1.3. Основные свойства неопределенного интеграла
1. Производная неопределенного интеграла равна подынтегральной функции:
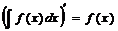
2. Дифференциал неопределенного интеграла равен подынтегральному выражению:
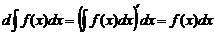
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная:
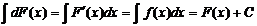
4. Постоянный множитель можно выносить за знак интеграла: 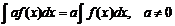
5. Неопределенный интеграл от суммы двух функций равен сумме их интегралов:

Справедливо для любого количества слагаемых. Необходимо помнить, существуют ли все функции на одном и том же множестве.
Таблица основных интегралов
1.  | 13.  |
2.  | 14.  |
3.  | 15.  |
4.  | 16.  |
5.  | 17.  |
6.  | 18.  |
7.  | 19.  |
8. 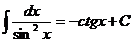 | 20.  |
9.  | 21.  |
10.  | |
11. 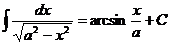 | 22. Для сложной функции:  |
12. 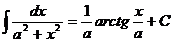 |
 2018-01-08
2018-01-08 1628
1628
