1. Исследуем на сходимость ряд 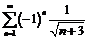 . Для этого рассмотрим абсолютные величины членов исходного ряда
. Для этого рассмотрим абсолютные величины членов исходного ряда 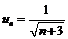 .
.
При этом 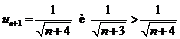 или
или 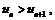 поэтому члены заданного ряда монотонно убывают по абсолютной величине. Кроме того,
поэтому члены заданного ряда монотонно убывают по абсолютной величине. Кроме того, 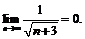 Выполнены все условия признака Лейбница, следовательно ряд сходится.
Выполнены все условия признака Лейбница, следовательно ряд сходится.
2. Найдем радиус сходимости степенного ряда 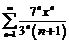 и определим характер сходимости ряда на концах интервала сходимости. По формуле
и определим характер сходимости ряда на концах интервала сходимости. По формуле 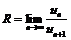 найдем радиус сходимости:
найдем радиус сходимости:
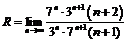
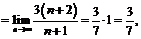
где 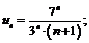
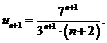 Тогда в интервале
Тогда в интервале 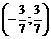 ряд сходится абсолютно. Выясним вопрос сходимости ряда на концах интервала, т. е. в точках
ряд сходится абсолютно. Выясним вопрос сходимости ряда на концах интервала, т. е. в точках 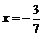 ,
,  . При
. При 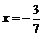 заданный ряд принимает вид
заданный ряд принимает вид
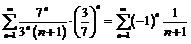 .
.
Это числовой знакочередующийся ряд. Его общий член по абсолютной величине монотонно убывает и стремится к нулю при n®¥. Таким образом, все условия признака Лейбница выполнены и ряд сходится, т.е. точка 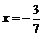 принадлежит области сходимости заданного ряда. При
принадлежит области сходимости заданного ряда. При  исходный ряд принимает вид
исходный ряд принимает вид 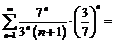
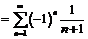 .
.
Это числовой знакоположительный ряд, который, очевидно, расходится (сравните его с гармоническим рядом). Следовательно, точка  не принадлежит области сходимости заданного ряда. Таким образом, область сходимости данного степенного ряда
не принадлежит области сходимости заданного ряда. Таким образом, область сходимости данного степенного ряда 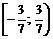 . Вне этого интервала ряд расходится.
. Вне этого интервала ряд расходится.
Задание 14
Задачи 261–280. Требуется: а) исследовать на сходимость с помощью признака Лейбница знакочередующийся ряд; б) найти радиус сходимости степенного ряда и определить тип сходимости ряда на концах интервала сходимости.
261. 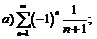
| 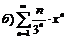 . .
|
262. 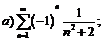
| 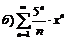 . .
|
263. 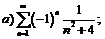
| 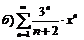 . .
|
264. 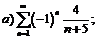
| 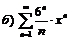 . .
|
265. 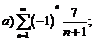
| 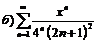 . .
|
266. 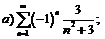
| 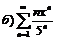 . .
|
267. 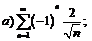
| 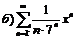 . .
|
268. 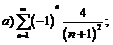
| 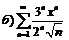 . .
|
269. 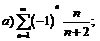
| 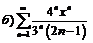 . .
|
270. 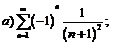
| 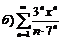 . .
|
271. 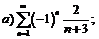
| 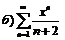 . .
|
272. 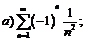
| 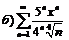 . .
|
273. 
| 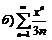 . .
|
274. 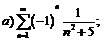
| 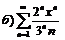 . .
|
275. 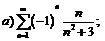
| 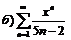 . .
|
276. 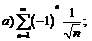
| 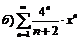 . .
|
277. 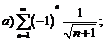
| 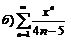 . .
|
278. 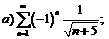
| 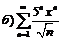 . .
|
279. 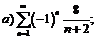
| 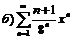 . .
|
280. 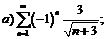
| 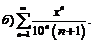
|
 2018-01-08
2018-01-08 518
518








