1. Найдем область определения функции

и изобразим ее геометрически.
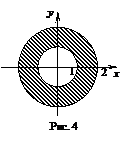 Область определения данной функции определяется системой неравенств
Область определения данной функции определяется системой неравенств

Построим границы области определения:
х 2+ у 2=1 – окружность R =1, центр (0;0);
х 2+ у 2=4 – окружность R =2, центр (0;0);
х 2+ у 2³1 – окружность R=2, центр (0;0);
x 2+ y 2³1 – внешняя часть круга радиуса 1;
x 2+ y 2£4 – внутренняя часть круга радиуса 2.
Областью определения данной функции является изображенное кольцо, границы которого входят в область определения функции.
2. Исследуем данную функцию на экстремум: Z =2 x 2– xy + y 2–3 x – y +1; x ÎR, y ÎR.
Найдем частные производные первого порядка:
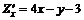 ;
; 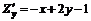 .
.
Найдем стационарные точки: 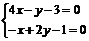 , откуда x =1, y =2.
, откуда x =1, y =2.
Таким образом, стационарной точкой функции является М(1; 2).
Проверим достаточные условия существования экстремума функции. Для этого найдем значения частных производных второго порядка:
 ;
; 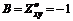 ;
;  .
.
Составим выражение AC–B2 =4×2–(–1)2=7>0 – экстремум существует. Так как А =4>0, то функция в точке М имеет минимум.
Z min(1; 2) = 2×12–1×2+22 –3×1–2+1=2–2+4–3–2+1=0, Z min=0.
Задание 11
Задачи 201-220. Найти область определения функции двух переменных и изобразить ее геометрически.
201. 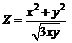 . .
| 202. 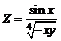 . .
|
203.  . .
| 204. 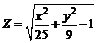 . .
|
205.  . .
| 206. 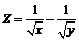 . .
|
207.  . .
| 208.  . .
|
| 209. Z =arcsin (x + y). | 210. Z =arcсos (x – y). |
211. 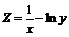 . .
| 212. 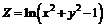 . .
|
213. 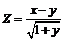 . .
| 214. 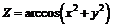 . .
|
215. 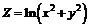 . .
| 216.  . .
|
217. 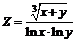 . .
| 218. 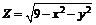 . .
|
219. 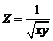 . .
| 220.  . .
|
Задание 12
Задачи 221–240. Исследовать на экстремум функции.
221. 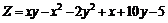 . .
|
222. 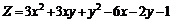 . .
|
223.  . .
|
224. 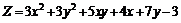 . .
|
225. 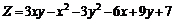 . .
|
226. 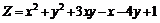 . .
|
227.  . .
|
228.  . .
|
229. 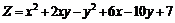 . .
|
230. 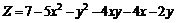 . .
|
231. 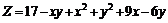 . .
|
232. 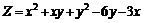 . .
|
233. 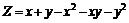 . .
|
234. 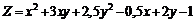 . .
|
235. 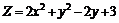 . .
|
236. 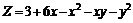 . .
|
237. 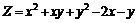 . .
|
238. 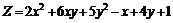 . .
|
239. 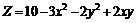 . .
|
240. 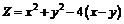 . .
|
Тема 9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Вопросы для самопроверки
1.Сформулировать теорему существования и единственности решения дифференциального уравнения.
2. Что называется общим решением, частным решением дифференциального уравнения?
3. Какой вид имеет дифференциальное уравнение с разделяющимися переменными?
4. Какой вид имеет общее решение линейного однородного уравнения второго порядка?
 2018-01-08
2018-01-08 509
509








