Оборудование и принадлежноси: лабораторная установка, набор грузов (гирь).
Лабораторная установка
Установка для измерения схематически показана на рис. 17.3. Исследуемый образец (резиновая трубка) 1 имеет на концах металлические
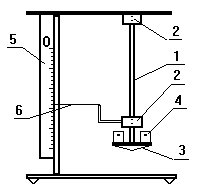
Рис. 17.3.
зажимы 2. Верхний зажим закреплен неподвижно к штативу, к нижнему зажиму подвешена платформа 3 для размещения гирь 4. Параллельно образцу закреплена линейка 5, нулевое деление которой совпадает с верхним концом образца. (За концы образца можно принимать внутренние концы зажимов). По нижней части линейки отмечается первоначальная длина (ненагруженного) образца. На шкале линейки 5 находится стрелка 6, основание которой закреплено на нижнем зажиме. При растяжении образца стрелка перемещается на величину абсолютного удлинения.
В нашем опыте роль внешней силы 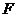 играет сила тяжести
играет сила тяжести  . Из определения напряжения
. Из определения напряжения  , закона Гука
, закона Гука 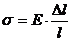 для цилиндрического образца диаметром
для цилиндрического образца диаметром 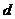 , искомое соотношение для модуля Юнга имеет вид:
, искомое соотношение для модуля Юнга имеет вид:
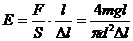 . (17.5)
. (17.5)
Методика измерения
1. При свободной от гирь платформе по шкале линейки найдите длину образца 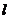 и начальное положение стрелки
и начальное положение стрелки  . Положение стрелки отмечают с точностью 0,5 мм.
. Положение стрелки отмечают с точностью 0,5 мм.
2. Ставьте на платформу грузы парами (симметрично подвесу во избежание перекоса). Каждый раз отмечайте показания стрелки удлинения 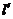 .
.
3. Результаты измерений занесите в таблицу по предложенной форме 17.1.
4. При максимальной нагрузке штангенциркулем измерьте диаметр образца. (Следите, чтобы штангенциркуль не зажимал резину, а лишь только касался ее поверхности). Так же измерьте начальный диаметр (ненагруженного образца).
5. Для проверки применимости закона Гука постройте графики зависимости модуля Юнга 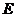 от напряжений
от напряжений 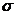 .
.
6. Рассчитайте ошибку определения модуля Юнга 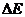 (достаточно рассчитать для одного опыта).
(достаточно рассчитать для одного опыта).
7. Значения модуля Юнга, совпадающие с учетом ошибки 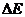 друг с другом, т.е. не выходящие за границы значений
друг с другом, т.е. не выходящие за границы значений 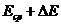 и
и 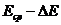 , позволяют определить истинное (среднее) значение модуля Юнга.
, позволяют определить истинное (среднее) значение модуля Юнга.
8. С учетом п.7 определить среднее значение модуля Юнга.
9. Используя те же значения, что и в п. 8, определить среднее значение коэффициента Пуассона.
10. Ошибка модуля Юнга 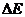 определяется из рабочей формулы (17. 5) как сумма частных ошибок всех величин, входящих в выражение:
определяется из рабочей формулы (17. 5) как сумма частных ошибок всех величин, входящих в выражение:
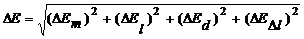 , где
, где
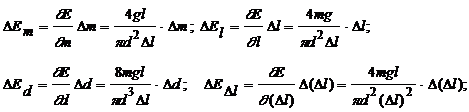
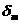 ,
, 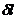 ,
, 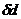 ,
, 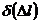 - абсолютные погрешности определения соответствующих величин.
- абсолютные погрешности определения соответствующих величин.
Форма 17.1
| Измеряемая и рассчитываемая величина | Ненагруженный образец | 1-й груз | 2-й груз | 3-й груз | 4-й груз | 5-й груз |
| Масса груза m, кг | ||||||
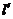 , мм , мм | ||||||
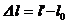 , мм , мм | ||||||
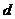 , мм , мм | ||||||
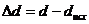 , мм , мм | ||||||
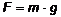 , Н , Н | ||||||
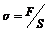 , , 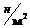 | ||||||
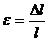 | ||||||
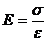 , ,  | ||||||
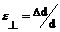 | ||||||
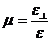 |
Контрольные вопросы
1. Что такое коэффициент упругости, модуль Юнга?
2. Что такое абсолютное и относительное удлинение образца?
3. Что такое механическое напряжение?
4. Что такое коэффициент Пуассона?
5. Что такое абсолютное и относительное поперечное сжатие?
6. Какие из перечисленных характеристик относятся к материалу?
7. Какие из перечисленных характеристик относятся к образцу?
8. Закон Гука и его физический смысл.
9. Кривая зависимости 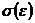 и ее характерные точки и участки.
и ее характерные точки и участки.
10. Деформация сдвига, иллюстрация пластических деформаций.
11. В чем состоит суть данного метода измерения 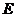 ?
?
12. Размерность 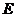 и
и 
13. Порядок величин 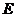 для различных твердых тел
для различных твердых тел
14. Учитывается ли в опыте масса самого стержня?
15. Почему мы не определяем величины 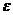 и
и  для сталей?
для сталей?
Используемая литература
[1] §14; [7] §21; [4] §48.
Лабораторная работа 1-18 “Изучение свободных колебаний пружинного маятника”
Цель работы: Определение жесткости пружины, определение периода свободных затухающих колебаний, логарифмического декремента затухания, коэффициента затухания.
 2018-01-08
2018-01-08 1181
1181








