2018-01-08
784
Среди различных тепловых свойств важное место занимает теплоемкость С, под которой для тела (или системы тел) понимают отношение
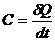(24.1)
где 
- бесконечно малое количество теплоты, полученное системой при повышении температуры на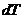 
.
Средняя теплоемкость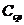 
в интервале температур от 
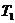до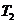 
может быть представлена таким образом:
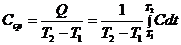, (24.2)
где 
- количество теплоты, за счет получения которой температура системы повысилась от 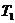до .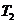
Так как количество сообщенной теплоты зависит от характера процесса (от пути процесса), определений (24.1) и (24.2) недостаточно, и необходимо указать, каким именно способом повышается температура. Действительно, если температура тела повышается вследствие адиабатического процесса, то 
и С=0. Если в системе происходит изотермический процесс, то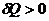 
или 
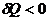, а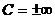 
.
Обычно на опыте имеют дело с двумя видами теплоемкостей: при постоянном давлении,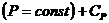 
, и при постоянном объеме, 
.
, 
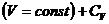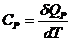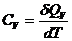, (24.3)
где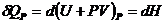 
, 
- энтальпия, а
, 
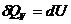- внутренняя энергия, а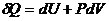 
- первое начало термодинамики.
Таким образом, теплоемкости 
и 
есть частные производные от энтальпии и внутренней энергии по температуре (при постоянных давлении и объеме). Уравнения
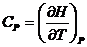и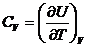 
(24.4)
можно рассматривать как определения. Они не имеют прямого отношения к теплоте и характеризуют зависимость энтальпии и внутренней энергии от температуры в условиях постоянного давления или объема и позволяют найти энтальпию или внутреннюю энергию системы при любой температуре, если известны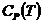 
и 
.
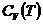Теплоемкости и связаны между собой простым термодинамическим соотношением:
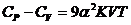(24.5)
где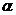 
- температурный коэффициент линейного расширения, 
- модуль всестороннего сжатия (см. определение в работе 1-23),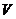 
- объем тела, 
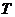- температура.
Относительная величина разности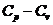 
для твердых тел невелика и ею можно пренебречь при невысоких температурах. Напомним, что в газах это не так: (
).
Чтобы теплоемкость вещества не зависела от массы тела вводят понятие удельной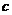 
и молярной теплоемкостей 
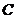. Удельная теплоемкость измеряется в 
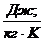, а молярная – в 
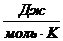. Из соображений размерности ясно, что 
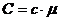, где 
- молярная масса вещества.
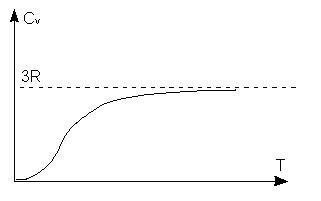
Рис. 24.1
Экспериментальные факты, относящиеся к теплоемкости типичных неорганических, химически простых, одноатомных кристаллических тел, можно свести к следующим пунктам.
1. При комнатных температурах значения теплоемкости таких веществ близки к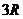 
, т.е. 
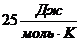. Это так называемый закон Дюлонга – Пти.
2. При низких температурах теплоемкость заметно уменьшается и в области абсолютного нуля температур приближается к нулю (рис. 24.1).
Эту особенность температурной зависимости теплоемкости твердого тела при низких температурах можно объяснить только с помощью квантовой теории (модели Эйнштейна и Дебая).
Методика измерений
Для экспериментального определения теплоемкости исследуемое тело помещается в калориметр, который нагревается электрическим током. Если температуру калориметра с исследуемым образцом очень медленно увеличивать от начальной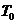 
на 
, то энергия электрического тока пойдет на нагревание образца и калориметра:
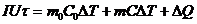(24.6)
где 
и - ток и напряжение нагревателя;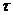 
- время нагревания; 
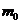и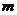 
- массы калориметра и исследуемого образца; 
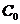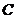, - удельные теплоемкости калориметра и исследуемого образца; 
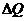- потери тепла в теплоизоляцию калориметра и в окружающее пространство.
Для исключения из уравнения (24.6) количества теплоты, расходованной на нагрев калориметра и потери теплоты в окружающее пространство необходимо при той же мощности нагревателя нагреть пустой калориметр (без образца) от начальной температуры 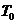на ту же разность температур .
Потери тепла в обоих случаях будут практически одинаковыми и очень малыми, если температура защитного кожуха калориметра в обоих случаях постоянная и равна комнатной: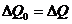 
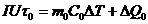(24.7)
Из уравнений (24.6) и (24.7) вытекает
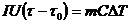(24.8)
Уравнение (24.8) может быть использовано для экспериментального определения удельной теплоемкости материала исследуемого образца. Изменяя температуру калориметра, необходимо построить график зависимости разности времени нагрева от изменения температуры исследуемого образца: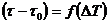 
, по угловому коэффициенту которого 
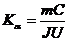можно определить удельную теплоемкость образца.
Экспериментальная часть.
Для определения теплоемкости твердых тел предназначена экспериментальная установка ФПТ1-8, общий вид которой показан на рис. 24.2.
Образцы нагреваются в калориметре, схема которого приведена на рис. 24.3.
Калориметр представляет собой латунный корпус с коническим отверстием, куда вставляется исследуемый образец. На наружной поверхности корпуса в специальных пазах размещается нагревательная спираль. Снаружи корпус калориметра теплоизолирован слоями асбеста и стекловолокна и закрыт алюминиевым кожухом. Калориметр закрывается теплоизолирующей крышкой. Исследуемые образцы расположены в гнездах в блоке рабочего элемента 2. После окончания эксперимента образец можно вытолкнуть из конического отверстия корпуса калориметра с помощью винта. Для удаления нагретого образца из калориметра и установки образца в нагреватель используется рукоятка, расположенная в специальном гнезде рядом с исследуемыми образцами.
Рисунок 24.2 - Общий вид экспериментальной установки ФПТ1-8: 1 - блок приборов; 2 - блок рабочего элемента; 3 - стойка; 4 - нагреватель; 5 - исследуемые образцы.
Температура калориметра измеряется цифровым термометром, датчик которого находится в корпусе калориметра. В блоке приборов 1 расположен источник питания нагревателя, мощность которого устанавливается регулятором «Нагрев». Напряжение и ток в цепи нагревателя измеряется вольтметром и амперметром, расположенными на передней панели блока приборов. Время нагрева калориметра измеряется секундомером, расположенным в блоке приборов. Секундомер приводится в действие при включении питания блока приборов.
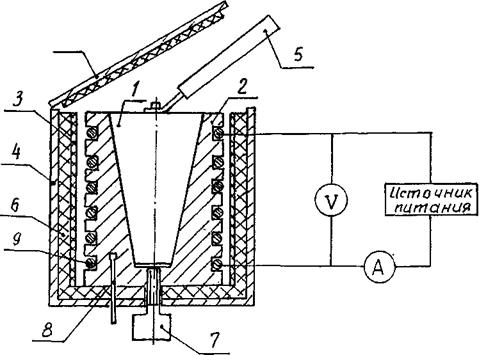
Рисунок 24.3 - Схема калориметра: 1 - образец; 2 - корпус, 3 - асбест; 4 - кожух; 5 - рукоятка; 6 - стекловолокно; 7 - винт; 8 - датчик температуры; 9 - нагреватель; 10 - крышка.
Массы образцов и относительные атомные массы материалов приведены в таблице 24.1.
Таблица 24.1
| № п/п | Материал образца | Атомная масса, кг/моль | Масса, г |
| Дюраль | 26,98 10-3 | ||
| Латунь | 63,57 10-3 | ||
| Сталь | 55,85 10-3 |
