2018-01-08
572
Структурний аналіз механізмів.
Заняття 3. Кінематичне дослідження механізмів
Задачі: 
Контрольні питання
1 Яка мета кінематичного дослідження механізму?
2 Які Вам відомі методи кінематичного дослідження механізмів?
3 Запишіть формулу залежності між швидкостями двох точок твердого тіла у плоскому русі.
4 Запишіть формулу залежності між пришвидшеннями двох точок твердого тіла у плоскому русі.
5 Запишіть формулу визначення швидкості точки у складному русі.
6 Запишіть формулу визначення пришвидшення точки у складному русі.
7 Як визначається модуль пришвидшення Коріоліса?
8 Як визначається напрямок пришвидшення Коріоліса? Правило Жуковського для визначення напрямку пришвидшення Коріоліса.
9 Що таке плани швидкостей та пришвидшень?
10 Як визначити модуль і напрямок кутової швидкості ланки за допомогою плану швидкостей?
11 Як визначити модуль і напрямок кутового пришвидшення ланки за допомогою плану пришвидшень?
12 Що таке миттєвий центр швидкостей?
|
|
|
13 Як визначити положення миттєвого центру швидкостей?
14 Як визначити швидкість будь-якої точки твердого тіла за допомогою миттєвого центру швидкостей?
15 Як читається теорема про проекції швидкостей двох точок твердого тіла на лінію, що їх з’єднує?
16 Як визначається модуль і напрямок нормального (доцентрового) пришвидшення?
17 Як визначається модуль і напрямок тангенціального (дотичного) пришвидшення?
Приклад 1.3
Визначити абсолютні швидкість та пришвидшення точки D кривошипного механізму з коливальним повзуном.
Дано: АВ=30 мм, АС=70 мм, ВD=120 мм, φ1=1500, кутова швидкість кривошипа АВ (ланка 1) стала величина і дорівнює ω1=15 с-1 (рисунок 1.7).
 |
Розв’язок
Креслимо механізм у положенні, що відповідає куту φ1= 1500.
1 Швидкість точки В ланки 1, яка обертається навколо нерухомої точки А:
Ланка 2 здійснює складний рух, що складається з переносного обертального руху разом з повзуном 3 навколо точки С і відносного поступального руху вздовж напрямляючої повзуна 3.
Вектор абсолютної швидкості точки В співпадає за напрямком з вектором 
. З іншого боку:
, (1.2)
де 
- вектор обертальної швидкості точки В навколо точки С2, геометрично співпадаючої з точкою С ланки 3;
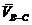- вектор відносної швидкості ковзання ланки 2 вздовж повзуна (точки С).
Рівняння (1.2) можна розв’язувати декількома методами. Визначимо положення ланки 2 відносно осі x. З трикутника АВС (рисунок 1.8)
1.1 З векторного трикутника, (див. рисунок 1.8), маємо
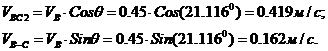
де 
Кутова швидкість ланки 2:
Для визначення швидкості точки D запишемо векторне рівняння:
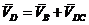. (1.3)
Тут вектор 
направлений перпендикулярно ланці ВD і має величину 
|
|
|
Спроектуємо векторне рівняння (1.3) на лінію ВD і на лінію перпендикулярну до неї:
2 Визначимо пришвидшення точки D.
 |
Пришвидшення точки В ланки 1, яка обертається навколо нерухомої точки А зі сталою кутовою швидкістю
:
.
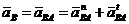Тут 
, а 
Пришвидшення точки В ланки 2:
(1.4)
Величина 
.
Вектор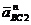 
направлений від точки В до точки С (див. рис.1.9).
Вектор 
направлений перпендикулярно ланці ВС, а вектор 
- вздовж цієї ланки. Напрямок пришвидшення Коріоліса визначається правилом Жуковського: щоб визначити напрямок пришвидшення Коріоліса для плоских механізмів треба відносну швидкість 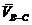повернути у напрямку кутової переносної швидкості 
на 900.
Величину пришвидшення Коріоліса визначимо за формулою:
Проектуємо рівняння (1.4) на осі координат 
:
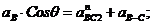
Звідки: 
Звідси ми бачимо, що пришвидшення має напрямок протилежний тому, який показано на рисунку 1.9 (закреслено і показано правильний напрямок).
Кутове пришвидшення ланки 2:
Напрямок кутового пришвидшення 
визначається пришвидшенням і в даному випадку буде проти руху годинникової стрілки.
Для визначення пришвидшення точки D запишемо рівняння:
(1.5)
Тут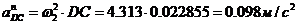 
.
Покажемо ці вектори на рисунку 1.9 і спроектуємо його на осі координат :
 |
3 Графоаналітичний метод.
3.1 Побудова плану швидкостей.
З точки 
- полюса плана швидкостей (див. рисунок 1.10), проведемо лінію, паралельну вектору 
і на ній відкладемо відрізок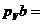 
45 мм. Цей відрізок зображає вектор з масштабним коефіцієнтом 
. Відповідно до рівняння (1.2), з точки в проводимо лінію перпендикулярно ланці ВС до пересічення з лінією, проведеною з точки паралельно ланці ВС. Точка пересічення позначена літерою с2. З’єднаємо її з полюсом.
Положення точки d на плані швидкостей визначимо з теореми подібності:
Звідки 
З’єднаємо точку d з полюсом.
Кутова швидкість ланки 2:
3.2 Побудова плану пришвидшень.
З точки π, полюса плана пришвидшень, проведемо промінь у напрямку вектора 
, на якому відкладемо відрізок 
.
Масштабний коефіцієнт побудови плану пришвидшень
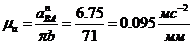
Відповідно до рівняння (1.4), з полюса π у напрямку пришвидшення 
проводимо відрізок
З точки в, напрямком у точку в, відкладаємо відрізок
З точки к проводимо лінію, паралельну вектору , до пересічення з лінією, проведеною з точки n, паралельно вектору 
. Точку пересічення позначимо с2.
.
Кутове пришвидшення ланки 2:
.
З’єднаємо точки в і с2. Точку d на плані пришвидшень знайдемо із співвідношень теореми подібності:
З’єднаємо точки d і π.
Пришвидшення точки D.
.
