2018-01-08
1289
Задачі: 
Контрольні питання
1 Яка мета кінетостатичного дослідження механізму?
2 В чому полягає умова статичної (кінетостатичної) визначеності кінематичного ланцюга?
3 Як визначається точка прикладання, величина і напрямок реакції в кінематичній парі п’ятого класу?
4 Як визначається точка прикладання, величина і напрямок реакції в кінематичній парі четвертого класу?
5 Чому група Ассура є статично визначеним кінематичним ланцюгом?
6 Дайте характеристику сил, що діють на механізм.
7 Як визначається величина і напрямок сили інерції?
8 Як визначається величина і напрямок момента сили інерції?
9 Як визначається точка прикладання, величина і напрямок рівнодіючої сили і момента сили інерції?
10 Запишіть умову рівноваги сил, що діють на групу Ассура.
11 Опишіть методику кінетостатичного розрахунку механізму аналітичним методом.
12 Опишіть методику кінетостатичного розрахунку механізму графо-аналітичним методом.
13 Як здійснюється кінетостатичний розрахунок вхідної ланки?
14 Опишіть порядок визначення зрівноважуючої сили методом М.Є.Жуковського.
15 Дайте визначення теореми Жуковського.
Приклад 1.6
Визначити реакції в кінематичних парах А, В, С і D шарнірного чотириланковика і зрівноважуючий момент Мз, прикладений до ланки АВ, якщо 
вісь ланки ВС горизонтальна, кути 
, сила прикладена до точки К, яка поділяє довжину ланки 
навпіл, 
, кут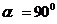 
(Рисунок 1.13).
Розв’язок
Відокремлюємо групу Ассура, що складається з ланок ВС і СD, і прикладаємо до неї діючі сили і реакції в’язів (рисунок 1.14). В обертальних кінематичних парах В і D реакції представимо у вигляді двох складових, які напрямляемо вздовж ланок (
) і перпендикулярно до них (
).
Складемо рівняння рівноваги:
З цих рівнянь: 
Для визначення нормальних складових реакцій складемо векторне рівняння суми усіх сил, що діють на групу Ассура в цілому:
Будуємо силовий многокутник відповідно до цього векторного рівняння. Відкладаємо силу Р3 у вигляді відрізка ав (рисунок 1.15). З точки в у напрямку вектора 
відкладемо відрізок 
. З кінця цього вектора (точки с) проведемо лінію паралельну вектору 
до пересічення з лінією, проведеною з точки а паралельно вектору 
. Точка перетину позначена буквою d. Враховуючи, що трикутник Δавс рівнобічний і прямокутний, маємо
і 
Реакція в точці D:
Розглядаючи ланку ВС, на яку діють дві сили 
і 
, бачимо, що 
Розглянемо вхідну ланку АВ (рисунок 1.16). До неї прикладена сила 
, реакція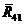 
з боку опори А і зрівноважуючий момент Мз.
Умови рівноваги сил, прикладених до ланки АВ:
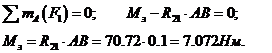
Приклад 1.7
Для кривошипного механізму з коливальним повзуном визначити зрівноважуючу силу Рз, прикладену до осі шарніра В перпендикулярно ланці АВ, та зрівноважуючий момент Мз, прикладений до ланки АВ, якщо в точці D ланки 2 прикладена сила Р2=20Н, перпендикулярно до лінії ВD. Кут 
, 
.
Розв’язок
Для визначення зрівноважуючої сили Рзр, використаємо метод Жуковського. Для цього будуємо план швидкостей, повернутий на 900 (рисунок 1.18), та прикладаємо до нього у відповідних точках сили Р2 і Рзр. Побудову плана швидкостей див. заняття 4.
Складемо рівняння моментів сил відносно полюса рV.
Кут
Зрівноважуючий момент
