Динамика продажи и цен товара

Период	Товарооборот, млн. руб.	Объем продажи, тыс. ед	Цена тыс. руб. за ед.	Цепные коэффициенты роста
товарооборота	продажи	цен
				-	-	-
				1,12	0,93	1,20
				1,24	0,57	2,17
				0,73	0,72	1,03
				0,60	0,43	1,40

 

Положение на рынке характеризуется падением спроса в результате роста цен на продукцию нефтяного машиностроения. Если до 3-го года рост цен обеспечивал увеличение валового дохода (товарооборота), то после него наметилась тенденция к его значительному сокращению, т.е. рост цен не смог компенсировать падение спроса. Товарооборот в 3-м периоде был в 1,24 выше предыдущего уровня и в 1,39 раза выше начального. В 5-м году рост цен превысил точку равновесия, и спрос стал коллапсировать (падать).

За анализируемый период объем продаж в натуральном выражении сократился за весь период более чем в 6 раз. Тенденция падения спроса моделируется уравнением тренда

660, 1 - 115,5 t,

т.е. спрос на товар постоянно сокращался в среднем на 115, 5 тыс. ед. изделий.

Рост цен за исследуемый период составил 373 %. Он также моделируется уравнением прямой, но с противоположной направленностью

2,4 + 10,4 t,

т.е. постоянный прирост цены составлял ежегодно 10, 4 тыс. руб.

Можно предположить, что в данной ситуации мы столкнулись с регрессирующим, мало перспективным рынком, требующим интенсивных маркетинговых усилий. Основным фактором падения спроса является рост цен. Модель зависимости объема продаж (y) от уровня цен (x) подтверждает этот факт

676, 8 -10, 8 x,

т.е. при увеличении цены на 1 тыс. руб. спрос на товар падает в среднем на 10, 8 тыс. ед. продукции.

В условиях экономики смешанного типа возрастает значимость прогнозирования жизненного цикла товара (ЖЦТ). Автором концепции ЖЦТ считается известный маркетолог Теодор Левитт, предложивший ее в 1965г.

Суть прогноза заключается в том, чтобы определить, как надолго и насколько интенсивно будет сохраняться спрос на данный товар. Прогноз ЖЦТ – многоплановый процесс, важной составляющей которого является подбор для каждого этапа соответствующей трендовой модели, отражающей не только рост, стабилизацию или спад, но и степень ускорения или замедления этих процессов. Такой прогноз является составным элементом прогнозирования покупательного спроса и рыночной конъюнктуры.

Жизненный цикл товара можно графически смоделировать в виде сложной кривой (рис. 1.2).

Математически смоделировать весь жизненный цикл товара практически невозможно, пришлось бы использовать сложную многочленную функцию, которую трудно интерпретировать. Целесообразно использовать метод линейно - кусочных агрегатов, то есть моделировать и прогнозировать каждый этап ЖЦТ с помощью трендовой и (или) многофакторной модели, отражающей закономерности каждого этапа.

 

 

1 – выведение товара на рынок; 2 – рост; 3 – зрелость; 4 – упадок; 5 – реанимация спроса

Рис. 1.2. Моделирование тенденции продажи товара по стадиям

Жизненного цикла

 

Отмеченные ранее методы механического выравнивания могут также выступать в роли самостоятельных методов статистического прогнозирования.

Прогнозирование на основе адаптивных скользящих среднихпроизводится с использованием следующих формул:

, (1.19)

где M_i – скользящая средняя, отнесенная к концу интервала;

. (1.20)

Первый член уравнения (3.19) – М_i-1 несет «груз прошлого» - инерцию развития, а второй адаптирует среднюю к новым условиям. Таким образом, средняя как бы обновляется, «впитывая» информацию о фактически реализуемом процессе (степень обновления определяется весом 1/m).

При прогнозировании с помощью экспоненциальных средних влияние прошлых наблюдений должно затухать по мере удаления от момента, для которого определяется средняя. Для этой цели используют экспоненциальное сглаживание, применяемое в краткосрочном прогнозировании (идея Н. Винера):

, (1.21)

где Q_t – экспоненциальная средняя на момент t;

a – коэффициент, характеризующий вес текущего наблюдения (параметр сглаживания).

При расчете по формуле (3.21) необходимо выбрать Q_{t- 1.}. Часто Q_{t- 1} принимают равным y_t.

Применение метода успешно, когда ряд имеет достаточно большое число уровней. Чем меньше a, тем больше роль «фильтра», поглощающего колебания 0< a £1. Практически диапазон a ограничивается величинами 0,1; 0,3. Хорошие результаты дает a = 0,1. При выборе a следует иметь в виду, что для повышения скорости реакции на изменение процесса развития необходимо повысить a, однако это уменьшает «фильтрационные» возможности средней. Пример расчёта скользящей средней представлен на рисунке П.3.1

Специфика экономических процессов состоит в том, что они обладают взаимосвязью и инерционностью. Последнее означает, что значение фактического показателя в момент времени t зависит определенным образом от состояния этого показателя в предыдущих периодах, т.е. значения прогнозируемого показателя должны рассматриваться как факторные признаки. Уравнение авторегрессионной зависимости в общем имеет вид

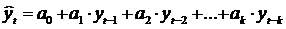, (1.22)

где – прогнозируемые значения показателя в момент времени t;

– значения показателя y в момент времени (t-i);

– i -тый коэффициент регрессии.

Часто прогнозируемый показатель зависит не только от предшествующих состояний, но и от других факторов x. Тогда говорят о смешанной авторегрессии:

(1.23)

Оценки a_i и b_j находят по МНК.

 

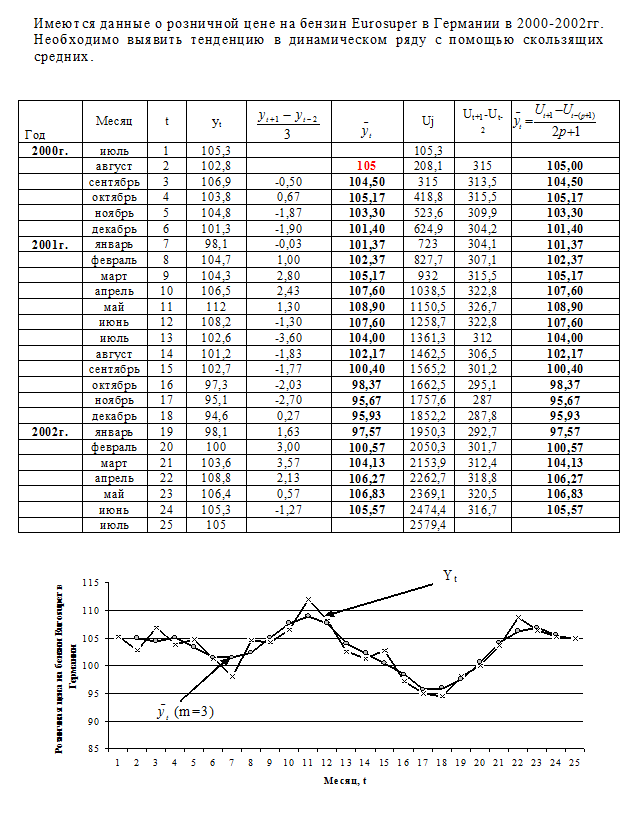
Рис. П.3.1 Расчёт скользящей средней с целью выявления тенденции

 

Все приведенные выше модели позволяют получить точечные оценки. Для определения наиболее вероятных интервалов варьирования прогнозных показателей необходимо найти доверительные оценки. В общем виде расчет доверительного интервала может быть представлен следующим образом:

 

, (1.24)

где – точечный прогноз;

– средняя квадратическая ошибка прогноза;

– t -статистика Стьюдента;

a – период упреждения прогноза.

В общем виде для полиномов различных степеней:

, (1.25)

где (Т¢×Т) – матрица системы нормальных уравнений;

– среднее квадратическое отклонение фактических значений от расчетных.

В частности, для линейного тренда

, (1.26)

где t_a – заданное на период упреждения значение переменной t, (t_a=n+a);

t – среднее значение t, т.е. значение порядкового номера уровня, стоящего в середине ряда;

– сумма квадратов отклонений значений независимой переменной от их средней.

Разработка прогноза методом экстраполяции (алгоритм решения задачи)

Шаг 1. Установить наличие и тесноту между величиной прогнозируемого показателя и фактором времени.

1.1. Определить точечную оценку коэффициента корреляции:

, (2.2)

 

где y_ti – текучее значение показателя y_t (t =1… n);

t_i – текучее значение показателя t (I = 1… n);

n – количество лет, за которые собранна статистика о значении показателя y_t.

 

1.2. Проверить значение коэффициента корреляции по критерию

 

(2.3)

 

(2.4)

 

где – коэффициент оценки достоверности гипотезы о значимости коэффициента парной корреляции (по табл. П.1.1, Приложение 1);

k = n-2 – число степеней свободы;

– вход в таблицу ;

– уровень значимости гипотезы.

При выполнении неравенства (2.3) гипотеза о незначимости коэффициента парной корреляции отвергается, т. е. величина y_t зависит от фактора времени.

По величине r_yt определяется сила взаимосвязи y_t и t при наличии между ними линейной связи. Чем ближе r_yt к +1 или –1, тем ближе связь между y_t и t к линейной. Наличие нелинейной связи определяется с помощью корреляционного отношения 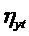(расчет см. далее).

Поскольку можно утверждать, что если r_yt = 0, 0, то в совокупности с графическим анализом зависимости y_t и t с помощью коэффициента парной корреляции можно оценивать наличие взаимосвязи, как при линейной, так и нелинейной корреляционной зависимости.

 

Шаг 2. Выбор вида математической модели, описывающей взаимозависимости y_t и t.

2.1. Построить график изменения показателя y_t на интервале [ t₁, t_n ].

2.2. Выбирать форму зависимости = f(t). Существует несколько практических подходов, которые позволяют более или менее удовлетворительно выбрать адекватную действительность динамики форму кривой. Наиболее простой путь – визуальный – выбор формы на основе графического изображения ряда динамики (шаг 2.1). Второй путь заключается в применении метода последовательных разностей, который описан в п.п.1.2 (см. формулу 2.5).

2.3. Расчет параметров тренда 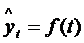, выбранного для экстраполяции, осуществляется по методу наименьших квадратов (МНК), сущность которого сводится к минимизации суммы квадратов отклонений фактических значений от расчетов (см. формулу 1.12).

Параметры уравнения тренда находят, решая системы нормальных уравнений. В приложении 2 (таблица П.2.2) приведены системы таких уравнений для некоторых форм зависимости.

Следует учитывать, что в практических исследованиях в основном используются следующие функции: линейная, показательная (экспонента), параболическая (2-го и 3-го порядка), гипербола. Поэтому при форме связи следует отдавать предпочтение именно этим зависимостям (для упрощения расчетов).

При выполнении вычислений на ЭВМ на практике осуществляется перебор всех подающихся вычислению моделей и производится выбор наилучшей из них. Лучшей считается та модель, для которой ниже приведенные критерии оценки точности принимают наименьшее значение (см. также п.п.2.2).

Шаг 3. Расчет критериев точности модели осуществляется в следующем порядке.

3.1. Определить расчетные значения моделируемого показателя , подставляя значения аргументов в полученное уравнение тренда.

3.2. Вычислить отклонение фактических значений y_t от расчетных

. (3.1)

 

3.3. Раcсчитать среднее квадратическое отклонение:

 

, (3.2)

 

где n – число наблюдений,

р – количество расчетных коэффициентов в уравнении тренда.

 

3.4 Определить среднюю относительную ошибку:

 

, (3.3)

 

Критерии (3.3) и (3.4) показывают степень точности воспроизведения моделью реального изменения моделируемого изменения моделируемого показателя.

Важным критерием надежности модели является эмпирическое корреляционное отклонение:

 

. (3.5)

 

где S² – общая дисперсия,

S² - остаточная дисперсия.

 

, (3.6)

где - математическое ожидание показателя, вычисленное по заданному динамическому ряду.

Корреляционное отношение характеризует тесноту связи между y_t и t при нелинейных зависимостях, его значения находятся в пределах от 0 до 1. Если зависимость линейна, то

 

. (3.7)

 

Это условие может быть использовано в качестве критерия линейности модели. Если условие выполняется, то линейность регрессии подтверждается.

 

Шаг 4. Прогнозирование показателя y_t.

4.1 Расчет точечной оценки прогноза показателя 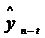осуществля-ется подстановкой величины t_i=n+1 в полученное уравнение тренда.

4.2 Расчет интервальной оценки прогноза осуществляется по зависимости

 

(3.8)

(3.9)

 

где t_jк – статистика Стьюдента определяемая по табл. П.1.1 приложение 1 по выходам k= n-2 и p = 1- ;

n – число наблюдений в динамическом ряду;

t_n+1 – величина t для прогноза года;

t – математическое ожидание t;

– среднее квадратическое отклонение фактических наблюдений y_t от расчетных 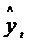(см. формулу 3.2).

В соответствии с вышеизложенной методикой осуществляется экстраполяционное прогнозирование технико-экономических показателей в соответствии с выбранным периодом упреждения.

Важно иметь в виду, что экстраполяция в рядах динамики носит приближенный и условный характер. Поэтому применение методов экстраполяции для выявления рыночных тенденций не должно становиться самоцелью, а при разработке экономических прогнозов должна привлекаться дополнительная информация, на основе которой в полученные методом экстраполяции количественные оценки вносятся соответствующие коррективы.

Пример выполнения расчётов при построении прогноза методом экстраполяции. Имеется динамический ряд экономического показателя y_t, характеризующего деятельность торгового предприятия (см. таблицу 5.1).

 

Таблица 5.1