Зворотня і транспонована матриці

Зворотну матрицю А ^-1, таку що А ^-1А=АА^-1=Е, де Е - одинична матриця, можна обчислити двома способами:

1) evalm(1/A);

2) inverse(A).

Транспонування матриці А – ця зміна місцями рядків і стовпців. Отримана в результаті цього матриця називається транспонованою і позначається А'. Транспоновану матрицю А' можна обчислити командою transpose(A).

Наприклад, використовуючи задану в попередньому пункті матрицю А, знайдемо зворотню до неї і транспоновану:

> inverse(A);

> multiply(A,%);

> transpose(A);

 

З'ясування типу матриці.

З'ясувати позитивну або негативну визначеність матриці можна за допомогою команди definite(A,param), де param може приймати значення: 'positive_def' – позитивно визначена (A>0), 'positive_semidef' –ненегативно визначена , 'negative_def' – негативно визначена (A<0 ), 'negative_semidef' - непозитивно визначена . Результатом дії буде константа true – підтвердження, false – заперечення зробленого припущення. Наприклад:

> А:=matrix([[2,1],[1,3]]);

> definite(А,'positive_def');

true

Перевірити ортогональність матриці А можна командою orthog(A).

> В:=matrix([[1/2,1*sqrt(3)/2]

[1*sqrt(3)/2, -1/2]]);

> orthog(В);

true

 

Функції від матриць.

Зведення матриці А в ступінь n проводиться командою evalm(A^n). Обчислення матричної експоненти можливо за допомогою команди exponential(A). Наприклад:

> Т:=matrix([[5*a,2*b],[-2*b,5*a]]);

> exponential(Т);

> evalm(Т^2);

 

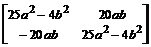
Завдання

1. Дані матриці:А, В, С. Знайти: (AB)С, detA, detB, detC, det[(AB)C].

2. Дана матриця, знайти: detA, A’, det(M22).

3. Знайти ранг матриці.

1. Обчислити, де Т(2, 2)_.

5. Дана матриця.А. Знайти значення многочлена.