Системы однородных линейных уравнений. Условие единственности решения

Однородные системы линейных уравнений

Однородная система линейных уравнений AX = 0 всегда совместна. Она имеет нетривиальные (ненулевые) решения, если r = rank A < n.

Для однородных систем базисные переменные (коэффициенты при которых образуют базисный минор) выражаются через свободные переменные соотношениями вида:

Тогда n - r линейно независимыми вектор-решениями будут:

а любое другое решение является их линейной комбинацией. Вектор-решения образуют нормированную фундаментальную систему.

В линейном пространстве множество решений однородной системы линейных уравнений образует подпространство размерности n - r; - базис этого подпространства.

 

 

Линейные пространства:определение,примеры.

Определение линейного пространства

Пусть V - непустое множество (его элементы будем называть векторами и обозначать ...), в котором установлены правила:

1) любым двум элементам соответствует третий элемент называемый суммой элементов (внутренняя операция);

2) каждому и каждому 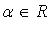отвечает определенный элемент (внешняя операция).

Множество V называется действительным линейным (векторным) пространством, если выполняются аксиомы:

I.

II.

III. (нулевой элемент, такой, что ).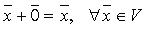

IV. (элемент, противоположный элементу ), такой, что

V.

VI.

VII.

VIII.