Пространство геометрических векторов. Операции с векторами и их свойства

Пространство геометрических векторов

Операции над векторами

Сложение

Операцию сложения геометрических векторов можно определить по разному, в зависимости от ситуации и типа расматриваемых векторов:

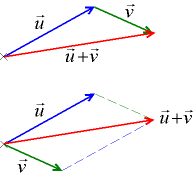
Два вектора u, v и вектор их суммы

Правило треугольника. Для сложения двух векторов 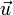и 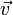по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.

Правило параллелограмма. Для сложения двух векторов 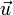и 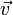по правилу параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.

А модуль (длину) вектора суммы 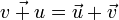определяют по теореме косинусов 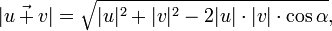где 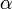— угол между векторами, когда начало одного совпадает с концом другого. Так же используется формула 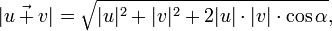теперь 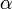— угол между векторами выходящими из одной точки.

Сложение двух скользящих векторов определено лишь в случае, когда прямые, на которых они расположены, пересекаются. Тогда каждый из векторов переносится вдоль своей прямой в точку пересечения этих прямых, после чего сложение осуществляется по правилу параллелограмма.

Сложение двух фиксированных векторов определено лишь в случае, когда они имеют общее начало. Их сложение в этом случае осуществляется по правилу параллелограмма.

Сложение коллинеарных скользящих векторов

Если скользящие векторы параллельны, то при их сложении главная трудность состоит в определении прямой, на которой будет расположена их сумма. (Величину и направление вектора суммы было бы естественно определить точно так же, как и в случае сложения свободных векторов.) В механике при изучении статики для решения вопроса о сложении параллельных сил, которые, как известно, задаются скользящими векторами, вводится дополнительная гипотеза: к системе векторов можно добавить два вектора, равных по величине, противоположных по направлению и расположенных на одной прямой, пересекающей прямые, на которых расположены данные вектора. Пусть, например, надо сложить скользящие векторы 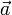и 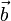, расположенные на параллельных прямых. Добавим к ним векторы 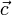и 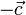, расположенные на одной прямой. 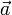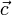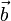Прямые, на которыхрасположены векторы и , и 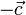пересекаются. Поэтому определены векторы

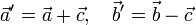
Прямые, на которых расположены векторы 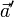и 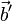, пересекаются всегда, за исключением случая, когда векторы 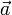и 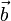равны по величине и противоположны по направлению, в котором говорят, что векторы 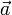и 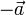образуют пару (векторов).

Таким образом, под суммой векторов 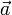и 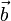можно понимать сумму векторов 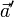и 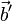, и эта сумма векторов определена корректно во всех случаях, когда векторы 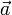и 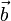не образуют пару.