Основная статья: Векторное произведение
Векторным произведением вектора 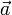 на вектор
на вектор 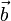 называется вектор
называется вектор 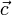 , удовлетворяющий следующим требованиям:
, удовлетворяющий следующим требованиям:
длина вектора 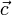 равна произведению длин векторов
равна произведению длин векторов 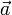 и
и 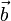 на синусугла φ между ними
на синусугла φ между ними
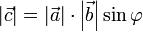
вектор 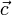 ортогонален каждому из векторов
ортогонален каждому из векторов 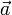 и
и 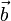
вектор 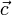 направлен так, что тройка векторов
направлен так, что тройка векторов 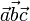 является правой.
является правой.
Обозначение: 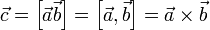
Геометрически векторное произведение 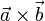 есть ориентированная площадь параллелограмма, построенного на векторах
есть ориентированная площадь параллелограмма, построенного на векторах 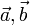 , представленная псевдовектором, ортогональным этому параллелограмму.
, представленная псевдовектором, ортогональным этому параллелограмму.
Свойства векторного произведения:
При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е 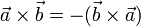
Векторное произведение обладает сочетательным свойством относительно скалярного множителя, то есть 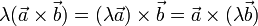
Векторное произведение обладает распределительным свойством: 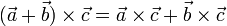
 2018-01-08
2018-01-08 395
395








