2018-01-08
561
Определение 10.10 Множество векторов на прямой назовем одномерным векторным пространством, множество векторов на плоскости -- двумерным векторным пространством, в пространстве -- трехмерным векторным пространством.
Легко проверить, что если 
-- какое-то векторное пространство, 
, 
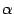-- число, то 
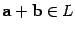и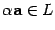 
.
Определение 10.11 Линейной комбинацией векторов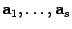 
с коэффициентами 
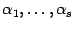называется вектор 
.
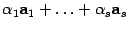Рис.10.10.Примеры линейных комбинаций
Векторы d, f, g на рисунке 10.10 и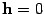 
являются линейными комбинациями векторов a, b, c: 
, 
, 
, 
.
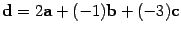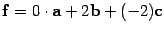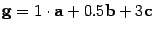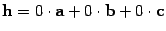Будем говорить, что вектор b раскладывается по векторам 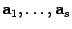, если b является линейной комбинацией этих векторов.
Координаты вектора
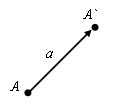
Есть вектора a. Пусть A (x; y) – начло вектора, а A` (x`; y`) – конец вектора. Координатами вектора a называются числа a1=x-x`, a2=y-y`. Для обозначения того, что вектор a имеет координаты a1 и a2, используют запись a (a1; a2) или (a1; a2).
Абсолютная величина вектора a (a1; a2) равна
Если начало вектора совпадает с его концом, то это нулевой вектор, обозначается (0).
|
|
|
