Опр. Пусть функция y = f (x) определена в точке х 0 и некоторой её окрестности. Функция f (x) называется непрерывной в точке х 0, если для "e>0 существует положительное число d, такое что для всех х из d-окрестности точки х 0 (т.е. если | х - х 0 |<d) выполняется неравенство | f (x) - f (х 0) |<e.

17. Точки разрыва и их классификация. Доказательство непрерывности функции многочлена и y=sin(x).
Для того, чтобы функция f (x) была непрерывной во внутренней точке х 0 области определения, необходимо и достаточно выполнение четырёх условий:
1) f (x) определена в точке х 0 (т.е. $ f (х 0)) и некоторой её окрестности;
2) $ 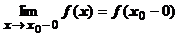 ; 3) $
; 3) $ 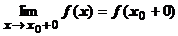 ;
;
4) Все эти три числа равны между собой: 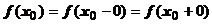
Опр. Если хотя бы одно из перечисленных условий непрерывности функции в точке не выполняется, f (x) называется разрывной в точке х 0, а сама точка х 0 называется точкой разрыва функции f (x).
Рассмотрим возможные варианты:
Опр. Точка разрыва х 0 называется точкой устранимого разрыва, если существуют одно-сторонние пределы 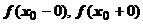 и они равны между собой (т.е. $
и они равны между собой (т.е. $ 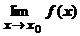 ).
).
Опр. Точка разрыва х 0 называется точкой разрыва первого рода (иногда применяется термин "скачок"), если существуют односторонние пределы 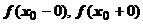 , но они не равны между собой.
, но они не равны между собой.
Опр. Точка разрыва х 0 называется точкой разрыва второго рода, если хотя бы один из односторонних пределов 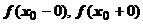 не существует.
не существует.
Теорема все элементарные функции непрерывны на своей области определения.

 2018-01-08
2018-01-08 2322
2322
