Теорема (о предельном переходе в неравенстве). Пусть функции f (x) и g(x) определены в проколотой окрестности  (x0) точки x0, причем для любого x
(x0) точки x0, причем для любого x  (x0) выполняется неравенство f (x)≥g(x). Тогда, если эти функции имеют пределы
(x0) выполняется неравенство f (x)≥g(x). Тогда, если эти функции имеют пределы  и
и  то a ≥ b.
то a ≥ b.
Доказательство. Пусть вопреки утверждению теоремы a < b, и пусть 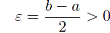 . Тогда существует δ1> 0 такое, что при 0 < |x — x0|<δ1 имеет место неравенство |f (x) — a| <ε, т.е. a — ε< f (x) < a + ε. Аналогично существует δ2> 0 такое, что при 0 < |x — x0| <δ2 выполняется неравенство |g(x) — b| <ε, т.е. b—ε< g(x) <b+ε.
. Тогда существует δ1> 0 такое, что при 0 < |x — x0|<δ1 имеет место неравенство |f (x) — a| <ε, т.е. a — ε< f (x) < a + ε. Аналогично существует δ2> 0 такое, что при 0 < |x — x0| <δ2 выполняется неравенство |g(x) — b| <ε, т.е. b—ε< g(x) <b+ε.
Если δ = min(δ1, δ2), и 0 < |x — x0| <δ, то 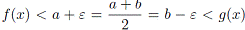 , т.е. f (x) < g(x) для указанных значений x — противоречие. Теорема доказана.
, т.е. f (x) < g(x) для указанных значений x — противоречие. Теорема доказана.
 2018-01-08
2018-01-08 7196
7196








