2018-01-08
3540
пусть a(х)®0, b(х)®0 при х ® а и пусть $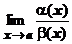 
.
Опр. Если 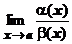- конечное число, отличное от нуля, то БМ функции a(х) и b(х) называются бесконечно малыми одного порядка.
Опр. Если 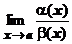=0, то БМ a(х) называется бесконечно малой более высокого порядка по сравнению с b(х) (b(х) называется бесконечно малой низшего порядка по сравнению с a(х)). Обозначение: a(х) = о(a(х)).
Опр. Если 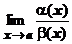=1, то БМ a(х) и b(х) называются эквивалентными. Обозначение: a(х)~b(х); если a(х)~b(х), то b(х)~a(х).
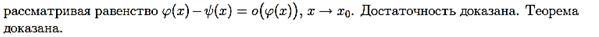
Теор. (Необходимое и достаточное условие эквивалентности ББ). Для того, чтобы ББ функции F (х) и G (х) были эквивалентными, необходимо и достаточно, чтобы выполнялось условие F (х) - G (х) = о(F (х)) (или F (х) - G (х) = о(G (х)).
Основная цель выделения главной части - получение более простой функции, которая в окрестности предельной точки ведёт себя также, как исходная.
При выделении главных частей указывается их вид; при решении задач на вычисление пределов при х ® а обычно это С0(х - а)k для бесконечно малых и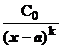 
для бесконечно больших, при х ®¥ - это 
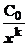для бесконечно малых и 
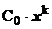для бесконечно больших, где С0 = const¹0, k =const>0 – порядок малости или роста функции f (x) относительно функции (х - а) (или относительно 
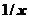при х ®¥). Для главных частей такого вида бесконечно малых при х ® а функций равносильны следующие утверждения:
|
|
|
1) 
;
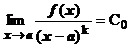2) 
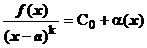, где a(х) – БМ при х ® а;
3) 
;
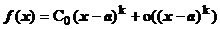4) 
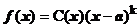, где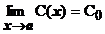 
;
5) f (x) ~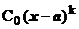 
.
Таким образом, в простейших случаях рецепт для выделения главной части вида С0(х - а)k БМ при х ® а функции f (x) состоит в следующем: f (x) надо представить в виде f (x)=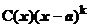 
, где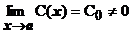 
. Тогда 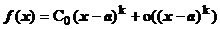, и 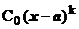- главная часть функции f (x) при х ® а. Аналогично с заменой (х - а)k
