Терема о дифференцируемости обратной функции (с доказательством)

Теор. Пусть для f (x): 1) выполняются условия Теоремы об обратной функции (непрерывность и строгая монотонность на отрезке [ a, b ]). 2) в точке х ₀ существует неравная нулю производная f' (х ₀). Тогда обратная функция х = g (у) в точке у ₀= f (х ₀) также имеет производную, равную . Док-во. Придадим переменной у приращение D у ¹0. Тогда переменная х получит приращение . Вследствие строгой монотонности D х ¹0; вследствие непрерывности D х ®0ÛD у ®0. . Устремим D у ®0, тогда D х ®0 и, по условию теоремы, существует (предел дроби), т.е. .

24. Дифференциал функции (определение, геометрический смысл). Инвариантность формы записи дифференциала первого порядка (с доказательством).

Опр. Главная часть приращения D у дифференцируемой функции, линейная относительно приращения D х аргумента (т.е. 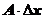), называется дифференциалом функции и обозначается dy (или df (x)). Дифференциал dy - это приращение ординаты касательной при смещении абсциссы на dх =D х.

Если х - независимая переменная, то формула для дифференциала: . Если , то . Таким образом, независимо от того, является ли х независимой переменной, или сама эта переменная х является функцией другой переменной t, формула для нахождения дифференциала первого порядка одна и та же. Это свойство и называется инвариантностью формы первого дифференциала.

25. Логарифмическая производная и производная функции, заданной параметрически.

(логарифмирование) Выведем формулу для производной показательно-степенной функции:

. Логарифмируем это выражение: . Дифференцируем обе части этого равенства по х, учитывая сложную зависимость от х в логарифмах:

.

Окончательно: .

Производные функций, заданных параметрически. Пусть зависимость у от х задана через параметр t: , обе эти функции дифференцируемы, и для первой из них существует обратная функция 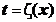. Тогда явная зависимость у от х выражается формулой . Находим производную: . Или:

26. Производные и дифференциалы высших порядков.

Производные высших порядков. Пусть функция имеет производную y' (x) в каждой точке интервала (а, b). Функция y' (x) тоже может иметь производную в некоторых точках этого интервала. Производная функции y' (x) называется второй производной (или производной второго порядка) функции и обозначается . Функция y'' (x) тоже может иметь производную, которая называетсятретьей производной (или производной третьего порядка) функции и обозначается 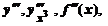. Вообще n -ой производной (или производной n -ого порядка) функции называется производная от производной (n -1)-го порядка (обозначения: ).

Дифференциалы высших порядков. Дифференциалом второго порядка (или вторым дифференциалом) функции называется дифференциал от её первого дифференциала; дифференциалом n -го порядка функции называется дифференциал от её (n -1)-го дифференциала. При вычислении высших дифференциалов необходимо учитывать, что дифференциал независимой переменной - произвольная и независимая от х величина, которая при дифференцировании рассматривается как постоянная. Поэтому ; ; …., .