Формулировки и доказательства теорем Ферма, Ролля, Лагранжа, Коши

28. Формулировка теоремы Бернулли – Лопиталя для предела отношения двух бесконечно малых или бесконечно больших функций (доказательство для случая отношения бесконечно малых). Раскрытие неопределенностей вида 0 ∙ ∞, ∞ – ∞, 0⁰, ∞⁰, 1^∞.

Неопределённость легко свести к неопределённост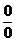и или : пусть f (x)®¥, g (x)®0 при х ® а. Тогда представление 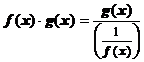даст неопределённость 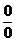, представление даст неопределённость

Неопределённость также можно свести к предыдущим случаям: если f (x)®¥, g (x)®¥ при х ® а, то ; дробь даёт неопределённость , если , получаем неопределённость 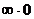, в других случаях неопределённость отсутствует.

Показательно-степенные неопределённости 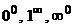с помощью представления приводятся к неопределённостям

29. Сравнение на бесконечности порядков роста показательной, степенной и логарифмических функций.
.

Предел найдём вначале в случае, когда - натуральное число. Применяя правило Лопиталя n раз, получим:

.

Пусть теперь b - произвольное вещественное число, b >0. Тогда n =E(b) £ b < n +1,

. Переходим к пределу при 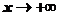. Пределы отношений, стоящих слева и справа, равны нулю; по теор. о пределе промежуточной функции .

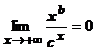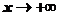
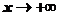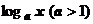Вывод: при = о(), =о() (), т.е. при ББ функция имеет более высокий порядок роста, чем ББ функции и ; ББ функция имеет более высокий порядок роста, чем ББ функция .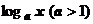

30. Вывод формулы Тейлора с остаточным членом в форме в форме Пеано и в форме Лагранжа (формулировка и доказательство соответствующих теорем).
Формула Тейлора для произвольной функции. Пусть теперь f (x) - произвольная функция, которая в точке х ₀ имеет производные всех порядков до n -го включительно. Построим с помощью производных этой функции многочлен Тейлора n -ой степени:

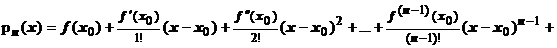
Значения этого многочлена и его производных до n -го порядка в точке х ₀ совпадают с производными функции f (x): = f (x ₀), , однако, если f (x) - произвольная функция, мы не можем утверждать, что ; многочлен 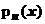лишь даёт некоторое приближение к f (x). Разность

называется остаточным членом формулы Тейлора и характеризует погрешность этого приближения.

Форма Пеано остаточного члена формулы Тейлора. Пусть для функции R_n (x) существуют все производные вплоть до n -го порядка и выполняются условия . Тогда при эта функция является бесконечно малой выше n -го порядка по сравнению с х - х ₀. (R_n (x) = о(х - x ₀) ⁿ)

Форма Лагранжа остаточного члена формулы Тейлора. Если в окрестности точки x ₀ существуют все производные функции f (x) до n +1-го порядка, можно получить другое представление остаточного члена: , где , точка с расположена между x и x ₀.

31. Формула Маклорена. Разложение по формуле Маклорена основных элементарных функций: е^x, sin(x), cos(x), 1n(1+x), (1+x)ⁿ.

Частный случай формулы Тейлора в случае x ₀ = 0 принято называть формулой Маклорена. Так, формула Маклорена с остаточным членом в форме Лагранжа такова:

, 0<q<1.

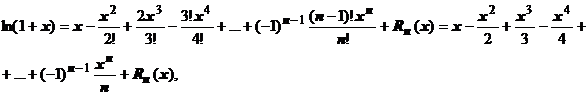
32. Необходимое и достаточное условия возрастания и убывания дифференцируемой функции (формулировки и доказательства).
Теор. Условие строгого возрастания (убывания) функции на интервале. Пусть функция имеет производную в каждой точке интервала 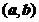. Для того, чтобы эта функция строго возрастала (убывала) на интервале 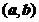, необходимо и достаточно, чтобы выполнялись условия:

1) ( ) для ; 2) не обращается тождественно в нуль ни на каком подынтервале этого интервала.

Док-во. Необходимость. Если f (x) строго возрастает (убывает), то, ( ) для ; при этом не обращается тождественно в нуль ни на каком подынтервале этого интервала, так как в этом случае 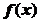была бы постоянной на этом подынтервале, что противоречит условию строгого возрастания (убывания).

Достаточность. Если выполняются условия теоремы, то, f (x) не убывает (возрастает). Предположим, что для двух точек и интервала 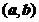значения функции равны: . Тогда, вследствие неубывания (невозрастания) f (x), для , т.е. 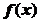постоянна на на этом интервале, что противоречит второму условию теоремы.

33. Понятие локального экстремума. Критические точки. Формулировка и доказательство необходимого условия локального экстремума дифференцируемой функции. Формулировка и доказательство достаточного условия локального экстремума функции по ее первой производной. Формулировка и доказательство достаточного условия локального экстремума функции по ее второй производной.
Опр.7.1. Пусть х ₀ - внутренняя точка области определения Х функции f (x), т.е. х ₀Î Х вместе с некоторой своей 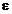-окрестностью. Точка х ₀ называется точкой (строгого) максимума функции f (x) (или f (x) имеет максимум в точке х ₀), если для любого х из проколотой 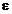-окрестности 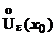этой точки выполняется неравенство f (x)< f (х ₀). (Если для выполняется 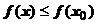, точка х ₀ называется точкой нестрогого максимума функции f (x)). Соответственно, точка х ₀ называется точкой (строгого) минимума функции f (x) (или f (x) имеет минимум в точке х ₀), если в некоторой проколотой окрестности этой точки для любого х Î выполняется неравенство f (x)> f (х ₀). Общее название для максимума и минимума функции - экстремум; точки, в которых достигается максимум или минимум - точки экстремума.

Опр. Точка области определения функции называется критической точкой первого рода этой функции, если: 1. в окрестности этой точки функция непрерывна; 2. в проколотой окрестности - дифференцируема; 3. в самой точке (конечная) производная функции равна нулю или не существует.

Опр. Точка называется критической точкой второго рода, если 1. непрерывна в некоторой окрестности ; 2. существует (конечная или бесконечная) производная функции в точке ; 3. дважды дифференцируема в некоторой проколотой окрестности точки ; 4. вторая производная этой функции в точке равна нулю или не существует.

Необходимое условие экстремума. Если во внутренней точке х области определения дифференцируемая функция 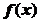имеет экстремум, то .

Первый достаточный признак экстремума (в критической точке, по знаку первой производной). Пусть точка - критическая точка первого рода функции , т.е. функция имеет производную в каждой точке некоторой проколотой окрестности точки , и пусть сохраняет определённый знак как справа, так и слева от точки (в отдельности). Тогда: если производная сохраняет знак при переходе через точку , то экстремум в этой точке отсутствует; если производная меняет знак при переходе через точку , то точка - точка экстремума, при этом если >0 при x < , <0 при x > , то - точка максимума, если <0 при x < , >0 при x > , то - точка минимума.

Второй достаточный признак экстремума (в стационарной точке, по знаку второй производной). Пусть функция в стационарной точке имеет не только первую, но и вторую производную. Тогда если , то - точка минимума, если , то - точка максимума.