Потенциал и разность потенциалов. Потенциал поля точечного заряда. Потенциал поля системы точечных зарядов. Эквипотенциальные поверхности

Потенциал – это энергетическая характеристика эл.стат. поля, скалярная физическая величина.

, где w – энергия взаимодействия пробного заряда с эл.стат. полем.

[φ] = Дж/Кл = В

Имеет смысл, как и для энергии взаимодействия, лишь изменение или разность потенциалов.

φ₁ - φ₂ = U

Для точечных зарядов:

Потенциал системы:

– алгебраическая сумма потенциалов от каждого заряда в отдельности.

Эквипотенциальные поверхности (Поверхности одного потенциала):

эти поверхности всегда перпендикулярны силовым линиям поля.

 

Градиент потенциала. Связь между градиентом потенциала и напряженностью эл.стат. поля.

U = φ₁ - φ₂ = (w₁-w₂)/q₊ = A_1-2/q₊; ().

-dφ=dw/q₊=dA/q₊

-dφ=Edr; dφ=-(

; ;

( =E_xdx + E_ydy + E_zdz

dφ=-( =-(E_xdx + E_ydy + E_zdz)

 

;

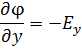
Градиент – математический оператор, grad = – векторная величина направленная в сторону противоположную напряженности эл.стат. поля.

Зная напряженность в каждой точке пространства, можно найти распределение потенциала dφ=-Edr, (dr - перемещение вдоль траектории)

, потенциал всегда определяется с точность до константы

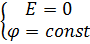
U=φ₁ – φ₂=

 

Связь между градиентом потенциала и напряженностью эл.стат. поля. Потенциал равномерно заряженной сферы.

φ₁ – φ₂=

Потенциал внутри заряженной сферы = потенциалу ее поверхности. Таким образом весь объем равномерно заряженной сферы эквипотенциальный, т.е. имеет одинаковый потенциал.