Векторный способ.
Пусть точка М движется по отношению к некоторой системе отсчета Oxyz. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор 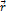 , проведенный из начала координат О в точку М
, проведенный из начала координат О в точку М
При движении точки М вектор 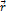 будет с течением времени изменяться и по модулю, и по направлению. Следовательно,
будет с течением времени изменяться и по модулю, и по направлению. Следовательно, 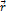 является переменным вектором (вектором-функцией), зависящим от аргумента:
является переменным вектором (вектором-функцией), зависящим от аргумента:
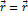 (t).
(t).
Равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор 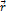 и найти положение движущейся точки.
и найти положение движущейся точки.
Геометрическое место концов вектора 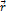 , т.е. годограф этого вектора, определяет траекторию движущейся точки.
, т.е. годограф этого вектора, определяет траекторию движущейся точки.
Координатный способ.
Положение точки можно непосредственно определять ее декартовыми координатами х, у, z (рис.1), которые при движении точки будут с течением времени изменяться. Чтобы знать закон движения точки, т.е. ее положение в пространстве в любой момент времени, надо знать значения координат точки для каждого момента времени, т. е. знать зависимости
|
|
|
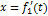 ,
, 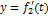 ,
, 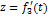 .
.
Уравнения представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения.
Разложим вектор 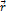 на составляющие по осям координат:
на составляющие по осям координат:
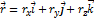 ,
,
где 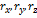 - проекции вектора на оси;
- проекции вектора на оси; 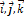 – единичные векторы направленные по осям, орты осей.
– единичные векторы направленные по осям, орты осей.
Так как начало 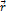 вектора находится в начале координат, то проекции вектора будут равны координатам точки M. Поэтому
вектора находится в начале координат, то проекции вектора будут равны координатам точки M. Поэтому 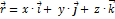
5. Скорость – это количественная характеристика движения тела.
Средняя скорость – это физическая величина, равная отношению вектора перемещения 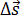 точки к промежутку времени Δt, за который произошло это перемещение. Направление вектора средней скорости совпадает с направлением вектора перемещения
точки к промежутку времени Δt, за который произошло это перемещение. Направление вектора средней скорости совпадает с направлением вектора перемещения 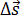 . Средняя скорость определяется по формуле:
. Средняя скорость определяется по формуле:
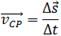
Мгновенная скорость, то есть скорость в данный момент времени – это физическая величина, равная пределу, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:
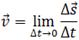
Иными словами, мгновенная скорость в данный момент времени – это отношение очень малого перемещения 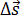 к очень малому промежутку времени, за который это перемещение произошло.
к очень малому промежутку времени, за который это перемещение произошло.
6. Равноме́рное движе́ние — механическое движение, при котором тело за любые равные отрезки времени проходит равные перемещения.(движение при котором ускорение равно нулю)
Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. 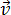 =
= 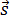 / t Ускорение - быстрота изменения скорости по велечине и по направлению.
/ t Ускорение - быстрота изменения скорости по велечине и по направлению. 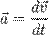
|
|
|
Центростремительное ускорение — компонента ускорения точки, характеризующая изменение направления вектора скорости для траектории с кривизной. 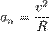 или
или 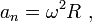
Тангенциа́льное ускоре́ние — компонента ускорения, направленная по касательной к траектории движения.
7. Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему.
Нормальное ускорение - это изменение скорости по направлению за единицу времени:
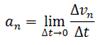
Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости.
Центростремительное ускорение – это нормальное ускорение при равномерном движении по окружности.
Полное ускорение при равнопеременном криволинейном движении тела равно:
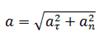
КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА.
Вращательным называется движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой – оси вращения.
а) Угловая скорость 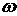 .
.
Быстрота вращения характеризуется угловой скоростью 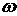 «омега», которая равна производной от угла поворота тела
«омега», которая равна производной от угла поворота тела 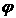 по времени
по времени 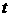
 ,
, 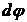 - угол поворота тела за малое время
- угол поворота тела за малое время 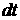 .
.
б) Угловое ускорение 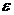 .
.
Угловое ускорение 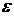 «эпсилон» равно производной от угловой скорости
«эпсилон» равно производной от угловой скорости 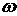 по времени
по времени 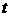 ,
,
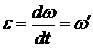 ,
, 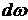 - изменение угловой скорости за время
- изменение угловой скорости за время 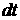 .
. 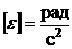 .
.
При ускоренном вращении тела направления векторов 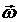 и
и 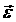 совпадают, при замедленном – противоположны.
совпадают, при замедленном – противоположны.
 2018-01-08
2018-01-08 1505
1505