2015-10-14
25789
Фундамент теоретической механики составляют законы механического движения, впервые сформулированные И. Ньютоном и положенные им в основу механики. Они представляют собой постулаты, суммирующие в сжатых формулировках наблюдения и опыт человечества; некоторые из них формулировались рядом ученых и до Ньютона, в частности Галилеем и Гюйгенсом.
Первый закон (закон инерции): изолированная от действия других материальных тел материальная точка сохраняет состояние покоя или равномерного прямолинейного движения.
Первый закон постулирует существование абсолютной или инерциальной системы отсчета перемещений, по отношению к которой изолированная точка покоится или совершает равномерное прямолинейное движение. При этом покой и равномерное прямолинейное движение равноправны и механически неотличимы. Способность материальных тел находиться в этих состояниях называется инерцией или инертностью.
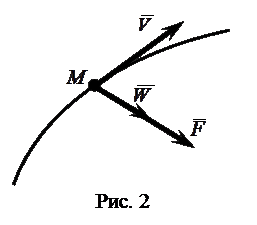
Второй закон (основной закон механики): сила, действующая на материальную точку, вызывает ускорение, пропорциональное этой силе по модулю и направленное вдоль линии ее действия (рис.2).
Этот закон выражается следующим уравнением:
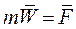. (2)
Здесь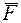 
– сила, действующая на точку; 
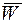– ускорение точки.
Следовательно, ускорение точки пропорционально силе и обратно пропорционально массе точки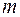 
. Данная сила вызывает тем меньшее ускорение точки, чем больше ее масса и наоборот, т. е. масса является мерой инерции точки, мерой ее способности сопротивляться изменению скорости (инертная масса). Уравнение (2) позволяет по известной силе и ускорению определить инертную массу точки.
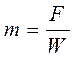. (3)
Опыт показывает, что гравитационная масса равна инертной.
Третий закон (закон равенства действия и противодействия): силы, с которыми действуют друг на друга две материальные точки, равны по модулю и направлены по прямой, соединяющей эти точки, в противоположные стороны (рис.3).
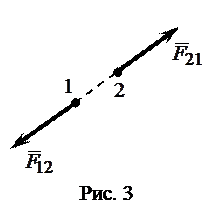
Иными словами, «действию» всегда соответствует равное по модулю и противоположное по направлению «противодействие». При этом нельзя говорить об их взаимном уравновешивании, так как «действие» и «противодействие» приложены к разным точкам.
Третий закон является основой механики механических систем. Он указывает источник силы, действующей на данное тело. Этим источником является другое тело (или силовое поле), которое, в свою очередь, находится под воздействием данного тела; итак, изменение движения данного тела может происходить лишь в результате его взаимодействия с некоторым другим телом (или полем). Если воздействие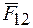 
второго тела на первое назвать «действием», а воздействие 
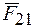первого на второе «противодействием», то согласно третьему закону
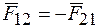, (4)
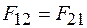. (5)
Четвертый закон (принцип независимости действия сил): если на материальную точку действует система сил, то ускорение точки равно геометрической сумме тех ускорений, которые точка имела бы при действии каждой силы в отдельности.
Этот закон выражается следующим уравнением:
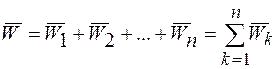, где 
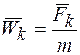(6);
а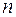 
– число сил, действующих на точку.
Четвертый закон позволяет вывести правило сложения сил, приложенных к одной материальной точке. Переписав равенство (6) в виде
,
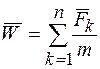и умножив обе части равенства на 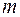, имеем
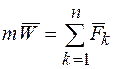, (7)
или
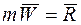. (8)
Сила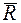 
, эквивалентная данным силам 
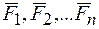и называемая равнодействующей этих сил, сообщает материальной точке то же ускорение 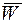, которое сообщают ей все силы от 
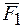до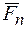 
, действуя совместно. Уравнение (7) или (8) называется основным уравнением динамики материальной точки. Из него следует соотношение:
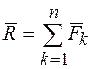, (9)
т. е. равнодействующая системы сил, приложенных к точке, равна их геометрической сумме.
Если к точке приложены две силы 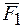и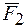 
, то они складываются по правилу параллелограмма (рис.4а), которое можно преобразовать в правило треугольника (рис. 4б). Последовательно распространяя правило треугольника на систему сил 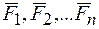, приложенных к точке, получаем правило силового многоугольника (рис. 4в). На рис. 4в 
. 
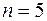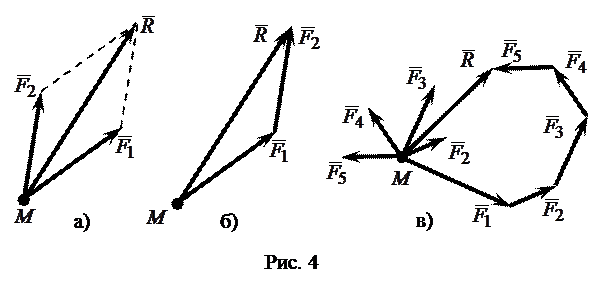
Из рис. 4в следует, что равнодействующая системы сил, приложенных к материальной точке, определяется замыкающей стороной силового многоугольника, построенного на данных силах.
Напомним следующую теорему векторной алгебры: проекция геометрической суммы векторов на координатную ось равна алгебраической сумме проекций составляющих векторов на ту же ось.
В заключение отметим, что рассмотренные законы механики справедливы в т.н. абсолютной или инерциальной системе отсчета.
