Фізичний зміст квадрата модуля хвильової функції
 (1.2.1)
(1.2.1)
де  ― функція, комплексно спряжена до
― функція, комплексно спряжена до  .
. 
В досліді Девіссона і Джермера встановлено, що струм, який реєструється гальванометром, пропорційний квадрату модуля хвильової функції  . (1.2.2)
. (1.2.2)
З іншого боку величина цього струму пропорційна також об’єму детектора dV  (1.2.3)
(1.2.3)
З урахуванням (1.2.2) і (1.2.3) маємо:  . (1.2.4)
. (1.2.4)
Якщо імовірність попадання частинок в детектор дорівнює dp, то величина струму гальванометра буде також пропорційною величині цієї імовірності I = k2dp. (1.2.5)
Прирівнявши рівності (1.2.4) і (1.2.5), одержимо:  . (1.2.6)Завжди можна вибрати значення хвильової функції таке, щоб k1=k2.
. (1.2.6)Завжди можна вибрати значення хвильової функції таке, щоб k1=k2.
Тоді (1.2.6) набуде вигляду  , (1.2.7) звідки
, (1.2.7) звідки
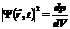 . (1.2.8)
. (1.2.8)
Квадрат модуля хвильової функції (1.2.8) визначає густину імовірності виявити частинку в точці з радіусом-вектором  в момент часу t. Квантова механіка на відміну від класичної дає імовірнісне пояснення квантового стану, а хвильова функція має статичний зміст.
в момент часу t. Квантова механіка на відміну від класичної дає імовірнісне пояснення квантового стану, а хвильова функція має статичний зміст.
При відомій хвильовій функції рівність (1.2.8) дозволяє визначити імовірність виявити частинку в об’ємі dV  . (1.2.9)
. (1.2.9)
|
|
|
Якщо частинка знаходиться у довільній точці простору, то ця подія є достовірною, а імовірність такої події дорівнює одиниці, тобто
 dV =1. (1.2.10)---умова нормування.
dV =1. (1.2.10)---умова нормування.
Рівняння руху квантової нерелятивістської частинки в силовому полі називається рівнянням Шредінгера, тому що вперше в 1926 році воно було сформульовано німецьким фізиком Е. Шредінгером.
У загальному випадку часове рівняння Шредінгера має вигляд
 (1.2.12)
(1.2.12)
де m ― маса частинки;  ― потенціальна енергія частинки в сило-вому полі;
― потенціальна енергія частинки в сило-вому полі;  ― уявна одиниця;
― уявна одиниця;  ― стала Дірака;
― стала Дірака; 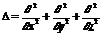 ― оператор Лапласа.
― оператор Лапласа.
Потенціальна енергія частинки залежить від координат x, y, z і часу t. Якщо потенціальна енергія U від часу не залежить і відповідно повна енергія також не змінюється з часом, то хвильову функцію  можна подати у вигляді добутку двох співмножників
можна подати у вигляді добутку двох співмножників  . (1.2.13)
. (1.2.13)
Підставляючи хвильову функцію (1.2.13) у рівняння Шредінгера (1.2.12) одержимо
 .
.
Скоротимо цей вираз на експоненту:  , (1.2.14)
, (1.2.14)
де  ; Е ― повна енергія частинки;
; Е ― повна енергія частинки;  ― потенціальна енергія частинки, яка є функцією лише координат;
― потенціальна енергія частинки, яка є функцією лише координат;  ― хвильова функція; m ― маса частинки;
― хвильова функція; m ― маса частинки;  ― стала Дірака (
― стала Дірака (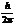 ).
).
При деяких значеннях повної енергії це рівняння може мати нульові розв’язки. Ті значення повної енергії, при яких рівняння (1.2.14) буде мати нульові розв’язки, називаються власними значеннями. Кожному такому власному значенню енергії відповідає свій розв’язок рівняння
 2018-01-08
2018-01-08 2240
2240








