Способи визначення понять
Спочатку виділяють невизначені поняття, на підставі яких визначаються математичні поняття наступними способами:
1) через найближчий рід і видову відмінність: а) дескриптивное (з'ясовує процес, за допомогою якого визначення побудовано, або описує внутрішню будову в залежності від тих операцій, за допомогою яких дане визначення було побудовано з невизначених понять), б) конструктивне (або генетичне), що вказує походження поняття.
Наприклад: а) прямокутник - це паралелограм, у якого всі кути прямі, б) колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки. Ця точка називається центром кола.
2) індуктивно. Наприклад, визначення арифметичної прогресії:
3) через абстракцію. Наприклад, натуральне число - характеристика класів еквівалентних множин;
4) аксіоматичне (непряме визначення). Наприклад, визначення площі фігури в геометрії: для простих фігур площа - це позитивна величина, чисельне значення якої має такі властивості: а) рівні фігури мають рівні площі, б) якщо фігура розбивається на частини, які є простими фігурами, то площа цієї фігури дорівнює сумі площ її частин; в) площа квадрата зі стороною, що дорівнює одиниці вимірювання, дорівнює одиниці.
Явні і неявні визначення
Визначення поділяються на:
а) явні, в яких чітко виділені визначається і визначають поняття (наприклад, визначення через найближчий рід і видову відмінність);
б) неявні, які будуються за принципом заміни одного поняття іншим з ширшим обсягом і закінчення ланцюжка є невизначені поняття, тобто формально-логічне визначення (наприклад, квадрат - ромб з прямим кутом; ромб - паралелограм з рівними суміжними сторонами; паралелограм - чотирикутник, з попарно паралельними сторонами; чотирикутник - фігура, що складається з 4 кутів, 4 вершин, 4 сторін).
Основна вимога при побудова визначень: визначається безліч повинно бути підмножиною мінімального множини. Наприклад, порівняємо два визначення: (1) Квадрат є ромб з прямим кутом, (2) Квадрат є паралелограм з рівними сторонами і прямим кутом (надлишкове).
Будь-яке визначення є рішення задачі на "доказ існування". Наприклад, прямокутний трикутник є трикутник з прямим кутом; його існування - побудова.
3. Означення та їх структура. Вимоги до означень.
Означення понять. Зміст поняття о будь-яком математичному об‘єкті містить багато різних суттєвих властивостей цього об‘єкта. Але щоб встановити, чи міститься об‘єкт в об‘ємі даного поняття (тобто разпознати його), необхідно перевірити наявність у нього лише деяких суттєвих властивостей. Встановлення цих суттєвих властивостей об‘єкта, яких достатньо для распознавння об‘єкта, називається означенням поняття про цей об‘єкт. Взагалі, означення – це логічна операція, яка розкриває зміст поняття. Способи означення поняття є різні. Перед усім розрізняють явні і неявні означення. Явні поняття мають форму рівності, спів падіння двох понять, або ототожнюються два поняття. Одне з них називають визначним поняттям, друге – визначальним. Ч ерез визначальне розкривається зміст визначного поняття. Проаналізуємо, наприклад, структуру означення квадрата: «Квадратом називається прямокутник, у якого всі сторони рівні». Вона є такою: спочатку вказане визначне поняття – «квадрат», а потім приведене визначальне, яке включає властивості: бути прямокутником, мати всі рівні сторони. Властивість «бути прямокутником» показує, що всі квадрати являються прямокутниками, тобто поняття прямокутник являється більш загальним, ніж поняття квадрат. Його називають родовим по відношенню до визначного поняття «квадрат». Друга властивість – «мати рівні сторони» - це виділення видової властивості, яка відокремлює квадрат від інших видів прямокутника. Схематично структуру таких означень можна представити наступним чином: МАЛЮНОК. Неявні означення не мають форми спів падіння двох понять. Прикладами таких означень являються так звані контекстуальні і остенсивні означення. В контекстуальних означеннях зміст нового поняття розкривається через уривок тексту, через контекст, через аналіз конкретної ситуації, яка описує зміст нового поняття. Прикладом такого означення може бути означення рівняння і його розв‘язок. Остенсивні означення використовують для введення термінів шляхом демонстрації об‘єктів, які цими термінами позначають. Тому остенсивні означення називають ще означеннями шляхом показу. Зустрічаються в математиці і означення, побудовані по іншому. Наприклад, означення трикутника: «Трикутником називається фігура, яка складається з трьох точок. Які не лежать на одній прямій, і трьох відрізків, які попарно з‘єднують ці точки». В цьому означенні вказане родове поняття по відношенню до трикутника – фігура, а потім вказаний спосіб побудови такої фігури, такі означення називають генетичними. Розглянемо означення арифметичної прогресії: «Арифметичною прогресією називається числова послідовність, кожний член якої, починаючи з другого, дорівнює попередньому, доданого з одним числом». Тут визначне поняття – «арифметична прогресія», родове поняття – «числова послідовність», а далі описується спосіб отримання всіх членів прогресії по заданій формулі. Таке означення називають індуктивним (рекурентним).
Вимоги до означень. Щоб оцінити правильність явних означень, необхідно знати правила означення понять.1) Перш за все визначне і визначальне поняття повинні бути еквівалентні (сорозмірні). Це означає, що сукупність предметів, які є охоплені ними, мають співпадати. Наприклад, правильним є означення: «прямокутник – це чотирикутник, у якого всі кути прямі». Неправильним означенням є таке:»Прямі 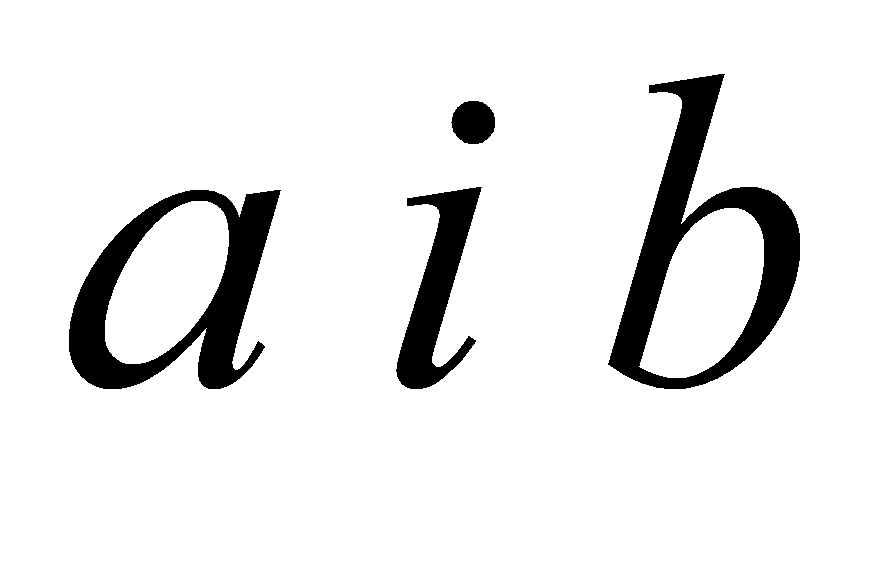 називаються паралельними, якщо вони не мають спільних точок або співпадають» (занадто широко, тому що йому задовольняють і мимобіжні прямі). Або невірним є: «прямі
називаються паралельними, якщо вони не мають спільних точок або співпадають» (занадто широко, тому що йому задовольняють і мимобіжні прямі). Або невірним є: «прямі 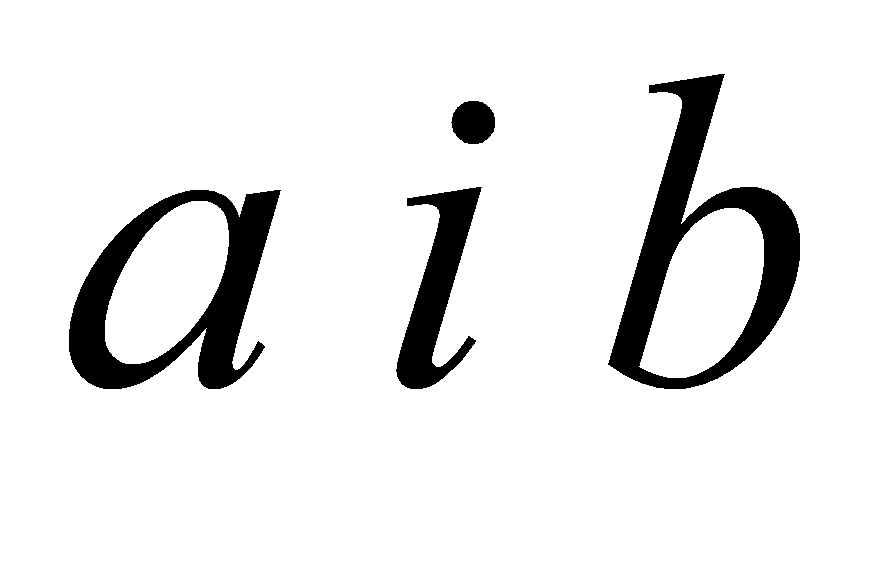 називаються паралельними, якщо вони не мають спільних точок» (занадто вузько, тому що йому не задовольняють прямі, які співпадають). 2) Друге правило означення забороняє порочний круг: не можна визначати поняття через само себе або визначати його через інше поняття, яке, в свою чергу, визначається через нього. Наприклад, множенням називається дія, за допомогою якої знаходять добуток цих чисел – неправильне означення. 3) В означенні мають бути вказані всі властивості, які дозволяють однозначно виділити об‘єкти, що належать об‘єму визначального поняття. Наприклад, «Суміжними кутами називаються кути, які в сумі складають
називаються паралельними, якщо вони не мають спільних точок» (занадто вузько, тому що йому не задовольняють прямі, які співпадають). 2) Друге правило означення забороняє порочний круг: не можна визначати поняття через само себе або визначати його через інше поняття, яке, в свою чергу, визначається через нього. Наприклад, множенням називається дія, за допомогою якої знаходять добуток цих чисел – неправильне означення. 3) В означенні мають бути вказані всі властивості, які дозволяють однозначно виділити об‘єкти, що належать об‘єму визначального поняття. Наприклад, «Суміжними кутами називаються кути, які в сумі складають 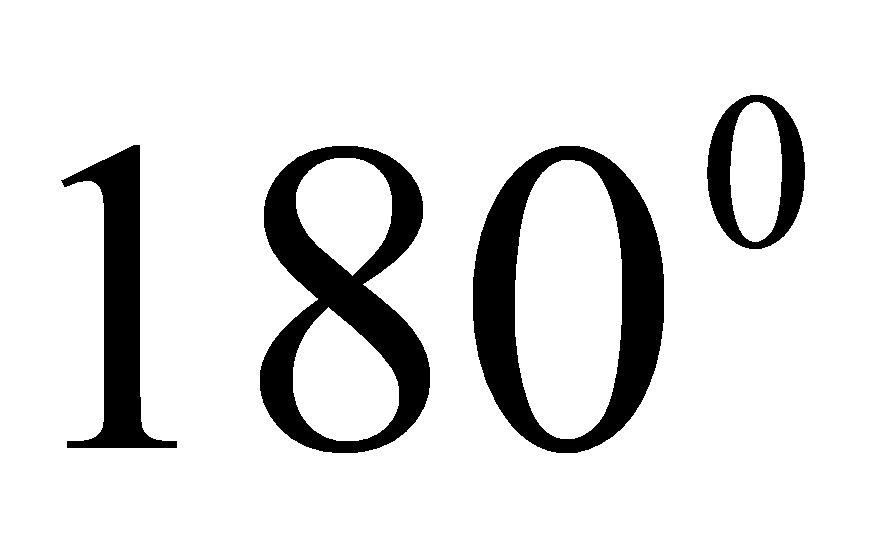 » (недостатньо властивостей). 4) Ще одне правило до означення – відсутність в ньому збитку. Це позначає, що в означенні не повинно бути вказано зайвих властивостей, які випливають з інших властивостей, також включених в означення поняття. Наприклад, «прямокутником називається чотирикутник, у якого всі сторони рівні і всі кути прямі».це означення має зайву властивість, краще сказати так: «Прямокутником називається чотирикутник, у якого всі кути прямі». Треба сказати, що в будь-якому означенні є елемент довільності, що проявляється, по-перше, в виборі терміна, а по-друге, в виборі властивостей, які включаються в означення. Якщо одному поняття дається два різних означення, то вони повинні бути рівносильними. Це позначає, що з властивостей, що включені в одне означення, мають випливати властивості, покладені в основу другого означення, і навпаки. При виборі означення користуються тим, яке означення простіше, натуральніше або корисніше для подальшої побудови теорії.
» (недостатньо властивостей). 4) Ще одне правило до означення – відсутність в ньому збитку. Це позначає, що в означенні не повинно бути вказано зайвих властивостей, які випливають з інших властивостей, також включених в означення поняття. Наприклад, «прямокутником називається чотирикутник, у якого всі сторони рівні і всі кути прямі».це означення має зайву властивість, краще сказати так: «Прямокутником називається чотирикутник, у якого всі кути прямі». Треба сказати, що в будь-якому означенні є елемент довільності, що проявляється, по-перше, в виборі терміна, а по-друге, в виборі властивостей, які включаються в означення. Якщо одному поняття дається два різних означення, то вони повинні бути рівносильними. Це позначає, що з властивостей, що включені в одне означення, мають випливати властивості, покладені в основу другого означення, і навпаки. При виборі означення користуються тим, яке означення простіше, натуральніше або корисніше для подальшої побудови теорії.
4.Висловлюванні форми. Висловлення із словами "всі", "деякі" (квантори).
Серед суджень, які встановлюють різноманітні відношення між математичними поняттями, вислови і висловлювані форми. Висловом називається твердження, відносно якого має сенс питання, істинно воно чи хибне. Наприклад, «число 6 парне» є істинним висловом, а «2+4=9» - хибним. Кожному вислову приписують одне з двох значень: І(істина), якщо воно істинне, і Х(хибність), якщо воно хибне. Значення І і Х називають значеннями істинності висловлення. Якщо висловлення елементарне, то його значення істинності визначають по змісту, спираючись на відомі факти. В складових висловленнях на допомогу приходить форма висловлення. Вважають, що вислів виду «А і В» істинний, якщо істинні обидва вислови А і В. якщо хоча б одне з них є хибним, то вислів «А і В» є хибним. Висловлення виду «А або В» вважають істинним, якщо істинний хоча б один з висловів А і В. Висловлення «А або В» хибне, коли хибні обидва вислови А і В. Часто в математиці приходиться будувати висловлення, в яких щось заперечується. Заперечення вислову 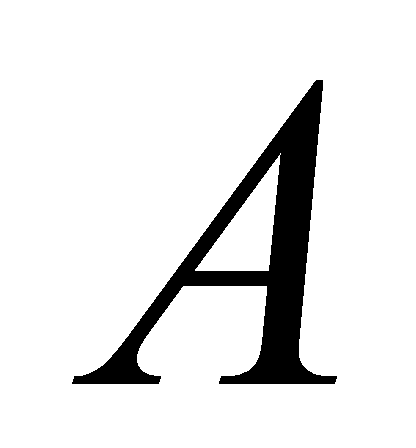 позначається
позначається  і читають «не А» або «невірно, що А». Взагалі запереченням вислову А вважається істинним, коли вислів А хибний, і «не А» є хибним, коли А істинний. ТАБЛИЦЯ.
і читають «не А» або «невірно, що А». Взагалі запереченням вислову А вважається істинним, коли вислів А хибний, і «не А» є хибним, коли А істинний. ТАБЛИЦЯ.
Висловлювані форми. В математиці часто зустрічаються твердження, які містять одну або декілька змінних. Наприклад, 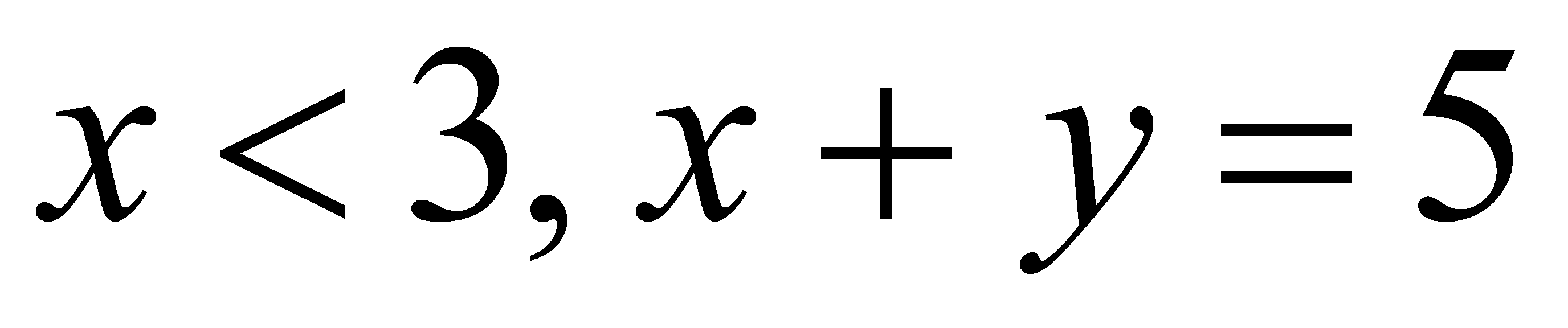 . Ці твердження не являються висловами, так як відносно їх не має сенсу питання, істинні вони чи хибні. Але при підстановці значень змінних ці твердження перетворюються в вислови істинні або хибні. Твердження такого виду називають висловлюваними формами. Кожна висловлювана форма породжує вислів тієї ж форми. Наприклад,
. Ці твердження не являються висловами, так як відносно їх не має сенсу питання, істинні вони чи хибні. Але при підстановці значень змінних ці твердження перетворюються в вислови істинні або хибні. Твердження такого виду називають висловлюваними формами. Кожна висловлювана форма породжує вислів тієї ж форми. Наприклад, 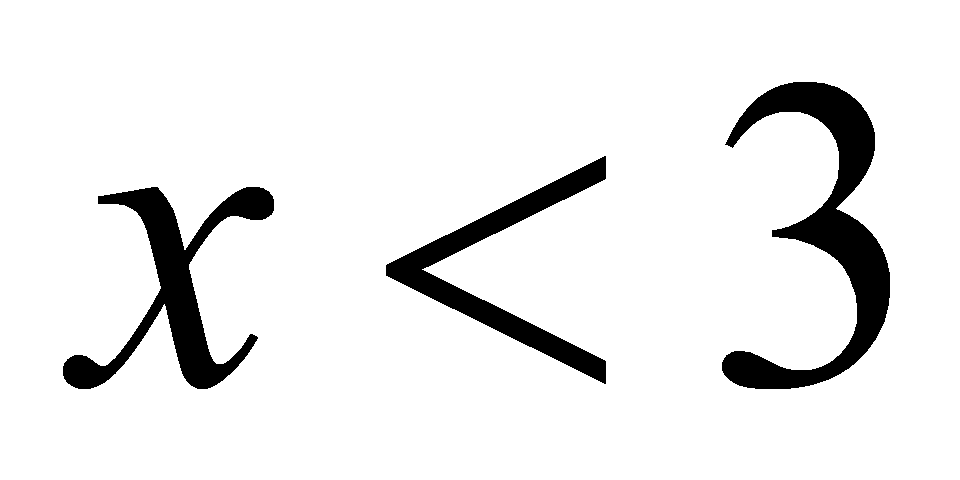 дозволяє отримати вислови
дозволяє отримати вислови 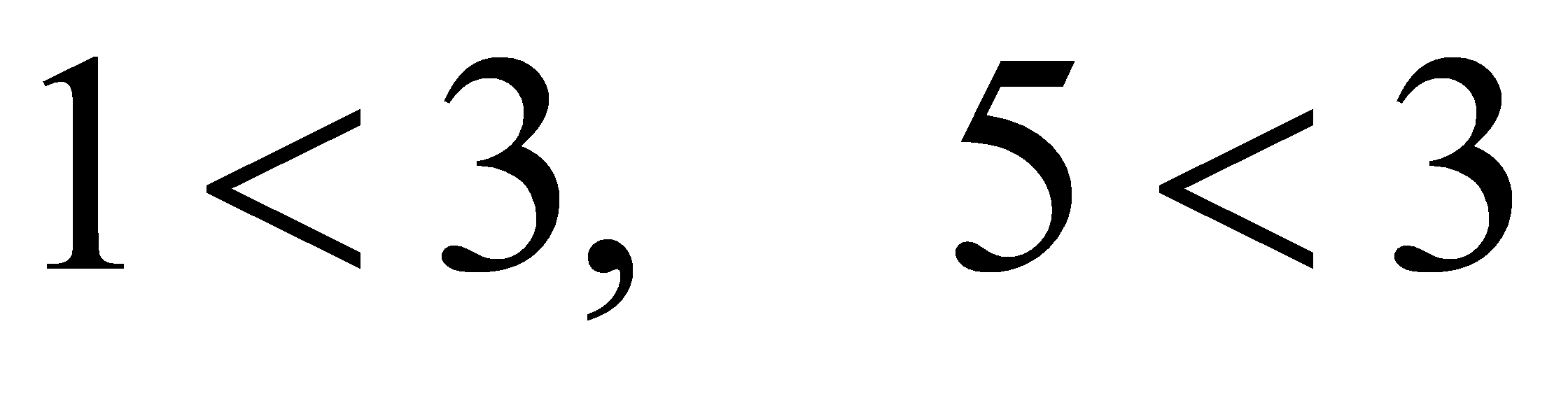 . Висловлювана форма – це твердження з однією або декількома змінними, яке обертається в висловлення при підстановці в нього конкретних значень змінних. Також як і висловлення, висловлювані форми бувають елементарними і складовими. Складові утворюються з елементарних за допомогою логічних зв‘язок «і», «або», «не» і т.д.
. Висловлювана форма – це твердження з однією або декількома змінними, яке обертається в висловлення при підстановці в нього конкретних значень змінних. Також як і висловлення, висловлювані форми бувають елементарними і складовими. Складові утворюються з елементарних за допомогою логічних зв‘язок «і», «або», «не» і т.д.
Квантори. Прочисла 0,1,2,3,4,5,6,7,8,9 можна сказати: всі подані числа однозначні і деякі з цих чисел є парними. Так як відносно цих тверджень можна сказати, що вони істинні чи хибні, то отримані твердження – висловлення. Слова «всі» і «деякі» називають кванторами. Слово квантор з латинського перекладається як «скільки», тобто квантор показує, о скількох (всіх або деяких) об‘єктах йдеться в твердженнях. Розрізняють квантори спільності і існування. Квантори спільності – це слова «будь-який», «всякий», «кожний», «всі». Квантори існування – це слова «існує», «деякі», «хоча б один». Таким чином, якщо перед висловлюваною формою поставити деякий квантор, то отримаємо вислів. Форму висловлення з квантором мають більшість математичних тверджень. Наприклад, всі квадрати являються прямокутниками; деякі парні числа діляться на 4; в будь-якому прямокутнику сума внутрішніх кутів дорівнює 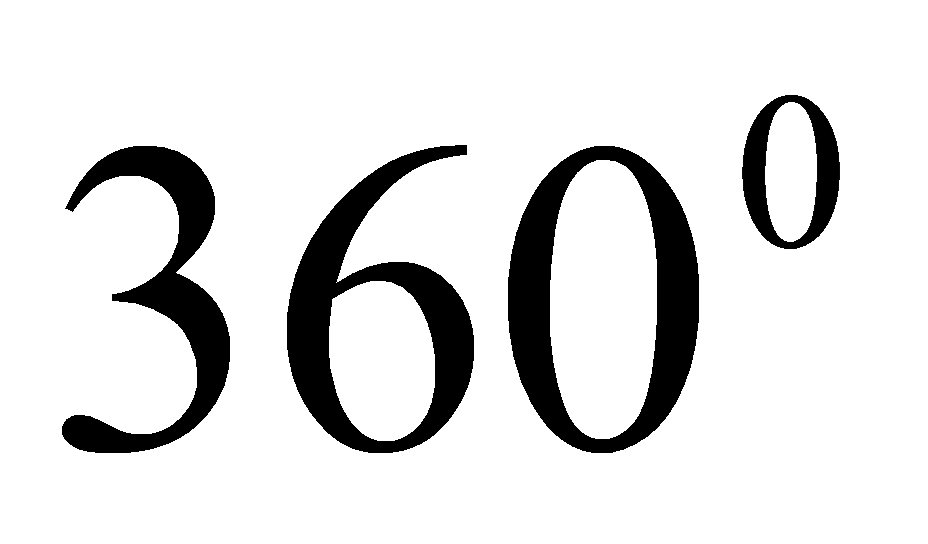 . Істинність висловів з кванторами спільності встановлюється шляхом доведення. Щоб впевнитися в хибності таких висловів, достатньо навести контр приклад. Наприклад, 1) Будь-яке число 0,1,2,3,4,5,6,7,8,9 являється розв‘язком нерівності
. Істинність висловів з кванторами спільності встановлюється шляхом доведення. Щоб впевнитися в хибності таких висловів, достатньо навести контр приклад. Наприклад, 1) Будь-яке число 0,1,2,3,4,5,6,7,8,9 являється розв‘язком нерівності 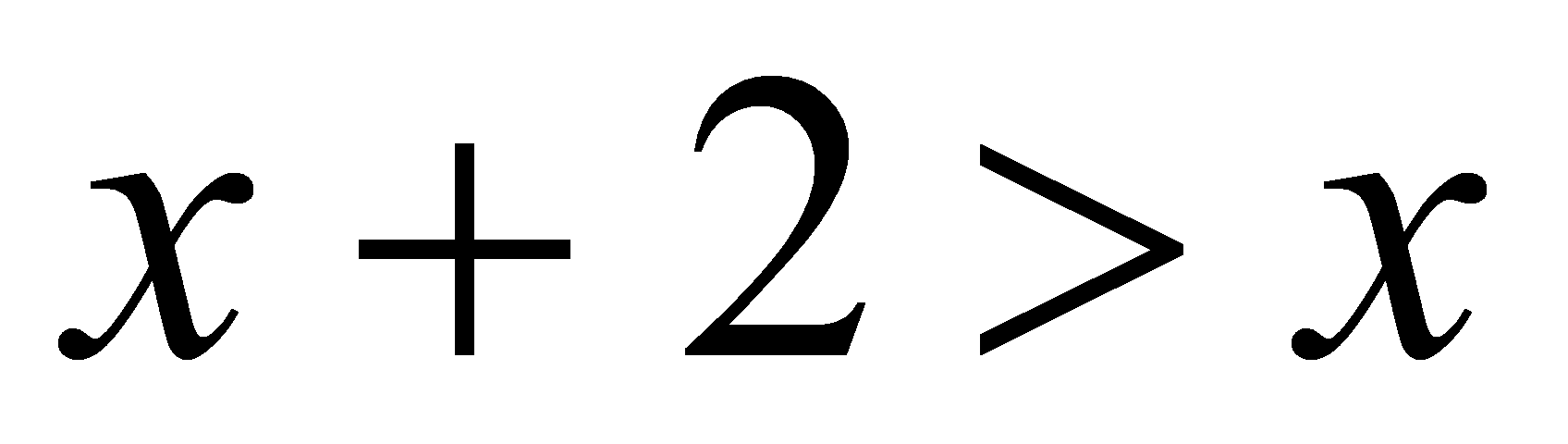 (підставляючи всі значення в нерівність довели істинність вислову, а значить, за індукцією, будь-яке дійсне число задовольняє нерівності). 2) Сума будь-яких послідовних натуральних чисел ділиться на 3 (істинність доводиться безпосередньо). 3) будь-який прямокутник являється квадратом (достатньо накреслити прямокутник, який не являється квадратом і доведена хибність вислову – контр приклад). Істинність висловів з кванторами існування встановлюється за допомогою конкретного прикладу. Щоб впевнитися в хибності такого вислову, необхідно провести доведення. Наприклад, 1) існують натуральні числа, кратні 3 (6, 9, 12 і т.д.). 2) Існують прямокутні рівносторонні трикутники (є хибним, тому що в прямокутному трикутнику один кут обов‘язково прямий, а в рівносторонньому всі кути містять
(підставляючи всі значення в нерівність довели істинність вислову, а значить, за індукцією, будь-яке дійсне число задовольняє нерівності). 2) Сума будь-яких послідовних натуральних чисел ділиться на 3 (істинність доводиться безпосередньо). 3) будь-який прямокутник являється квадратом (достатньо накреслити прямокутник, який не являється квадратом і доведена хибність вислову – контр приклад). Істинність висловів з кванторами існування встановлюється за допомогою конкретного прикладу. Щоб впевнитися в хибності такого вислову, необхідно провести доведення. Наприклад, 1) існують натуральні числа, кратні 3 (6, 9, 12 і т.д.). 2) Існують прямокутні рівносторонні трикутники (є хибним, тому що в прямокутному трикутнику один кут обов‘язково прямий, а в рівносторонньому всі кути містять 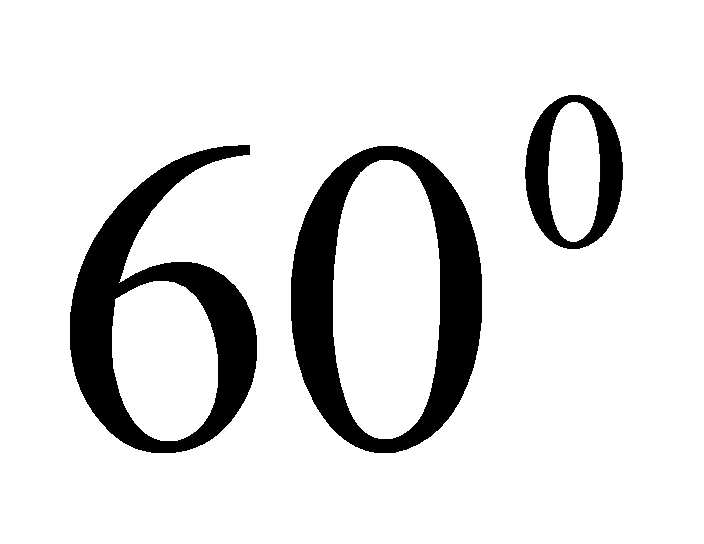 , значить, серед прямокутних трикутників рівносторонніх не існує).
, значить, серед прямокутних трикутників рівносторонніх не існує).
5.Правила побудови заперечень висловів, які містять квантори. Заперечення висловів з квантором (спільності або існування) може бути побудоване двома способами:
1) перед даним висловом ставляться слова «невірно що»; 2) квантор спільності (існування) замінюється квантором існування (спільності), а твердження, яке стояло після квантора, замінюється його запереченням. Сформульоване правило являється достатнім для правильної побудови заперечення висловів з квантором. Заперечення даного вислову може бути побудовано і в іншій формі. Важливо тільки не забути вимогу: якщо вислів хибний, то його заперечення повинно бути істинним, і навпаки. Наприклад, 1) «деякі непарні числа діляться на 4» -хибність, його заперечення: «невірно, що деякі числа діляться на 4», або «всі непарні числа не діляться на 4». 2) «всі натуральні числа діляться на 3» - хибність, його заперечення має вид: «невірно, що всі натуральні числа діляться на 3», або «існують натуральні числа, які не діляться на 3».
 В – необхідна умова для А А – достатня умова для В В – необхідна умова для А А – достатня умова для В |
 2018-01-08
2018-01-08 2299
2299
