2018-01-21
982
Функция распределения наработки до отказа
,
где 
– параметр формы распределения; 
– параметр масштаба распределения.
Плотность распределения наработки до отказа
.
При 
распределение Вейбулла совпадает с экспоненциальным
(рис. 3.1), когда интенсивность отказов постоянна.
При 
превращается в распределение Рэлея (рис. 3.6).
При 
интенсивность отказов монотонно возрастает (рис. 3.7).
При 
монотонно убывает (рис. 3.8).
 |
 |
|
 |
Средняя наработка до отказа
,
где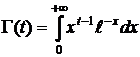 
– гамма-функция.
Среднее квадратическое отклонение
.
Распределение Вейбулла является достаточно универсальным, так как позволяет, варьируя его параметрами, добиваться различной формы кривой интенсивности отказов.
Гамма-распределение
Функция распределения наработки до отказа
,
где – параметр формы распределения; – параметр масштаба распределения; 
– гамма-функция Эйлера.
|
|
|
Плотность распределения
.
Средняя наработка до отказа
.
Среднее квадратическое отклонение
.
Графики показателей надёжности при гамма-распределении представлены на рис. 3.9.
 |
При интенсивность отказов возрастает, при убывает, а при становится постоянной, т.е. гамма-распределение превращается в экспоненциальное.
Гамма-распределение наиболее хорошо описывает распределение суммы независимых случайных величин, каждая из которых распределена по экспоненциальному закону.
При целом гамма-распределение называется распределением Эрланга порядка . Сумма случайных величин, имеющих экспоненциальное распределение с параметром 
, имеет распределение Эрланга с параметрами и 
. Функция распределения при этом будет иметь вид
.
Смесь распределений
Смесь распределений определяется, как линейная комбинация нескольких распределений. При этом выражения для основных показателей надежности будут иметь вид
,
,
,
,
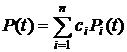где 
– коэффициент веса i -го показателя; 
.
Выбор того или иного закона распределения наработки до отказа определённого типа объектов должен основываться на анализе изменений их параметров на протяжении всего периода эксплуатации.
