Нормальное распределение (распределение Гаусса)

В отличие от экспоненциального, нормальное распределение используется для описания объектов, которые подвержены износу.

Функция распределения наработки до отказа

, (3.6)

где и – параметры нормального распределения.

Плотность распределения наработки до отказа

, (3.7)

Согласно (2.16) средняя наработка до отказа

. (3.8)

Графики показателей надёжности при нормальном распределении показаны на рис. 3.2.

 

Для практического использования соотношений (3.6) и (3.7) используется так называемое нормированное нормальное распределение. Перейдем от случайной величины наработки до отказа к иной случайной ве­личине

, (3.9)

имеющей математическое ожидание 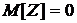и дисперсию .

Плотность распреде­ления величины 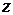следует из (3.7) и (3.9)

.

Соответственно функция распределения величины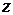

Графическое представление плотности распределение величины 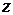показано на рис. 3.3.

Из графика очевидно, что функция является симметричной, т. е. , следовательно, .

 

Как правило, в справочной литературе приводятся значения не функции , а не­сколько иной функции

(3.10)

если ; если .

Функции и связаны между собой соотношением

(3.11)