Понятие потока отказов. Простейший (пуассоновский) поток

Поток отказов - это последо­вательность отказов, происходящих один за другим в случайные моменты времени.

Существует множество математических описаний потоков отказов. Наиболее распространённым из них является простейший (пуассоновский) поток отказов.

Простейший (пуассоновский) поток – это поток отказов, который одновременно обладает свойствами стацио­нарности, ординарности и отсутствия последействия.

Свойство стационарности. Поток называют стационарным, если числа отказов , , …, соответственно на отрезках времени , , …, зависят только от длительности этих отрезков , , …, и не зависит от выбора общего момента начала отрезков. В противном случае поток называют нестационарным. Выполнение требования стационар­ности означает, что вероятностные характеристики потока не зависят от вре­мени. В частности, закон распределения числа отказов на любом промежутке времени не зависит от самих значени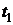й и , а зависит только от их разности .

Пример. Изменение во времени условий эксплуатации: температуры, вибрации, запылённости, квалификации обслуживающего персонала и других приводит к нестационарности.

Свойство отсутствия последствий. Поток отказов называют потоком без последействия, если для любого набора непересекающихся промежутков времени , , …, числа отказов на этих промежутках 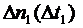, , 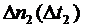…, представляют собой взаимно независимые случайные величины. В частности, выполнение требования отсутствия последействия означает, что распределение числа отказов на любом промежутке времени не зависит от течения потока до и после этого промежутка времени.

Пример. Последействия могут иметь место и из-за недостаточного качества вос­становления, когда свойства объекта не полностью регенерируются после отказа, а также в ситуации, когда отказ одного элемента вызывает ухудшение условий работы иных элементов.

Свойство ординарности. Поток называют ординарным,если

где 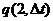- вероятность возникновения по меньшей мере двух отказов в те­чение промежутка времени длиной .

Ординарность означает практическую невозможность возникновения двух или более отказов одновременно.

Пример. Неординарность возникает в системе при условиях эксплуатации сверх допустимых пределов.

Вероятность возникновения 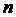отказов ( =0, 1, 2 …) на отрезке времени длиной определяется распре­делением Пуассона

(4.1)

где параметр распределения.