Расчёт по прочности сечений, наклонных к продольной оси, по поперечной силе

Максимальная поперечная сила от расчётной нагрузки:

Q_max=53,55кН

Определяем коэффициенты, характеризующие работу сечения:

φ_n= = 0,37˂0,5

N – усилие обжатия с учётом всех потерь(P₂)P₂=127,37кН

Проверяем, требуется ли поперечная арматура по расчёту.

Условие первое:

Q_max=53,55∙10³Н˂2,5 =2,5∙0,9(100)∙14∙27=85,05∙10³Н– условие удовлетворяется.

При q₁ = g + = 4,74+ = 11,523 кН/м = 115,23Н/см и поскольку

0,16∙ φ_b4(1+ φ_n) =0,16∙1,5∙1,37∙0,9(100)∙14 = 414,3Н/см> 115,23Н/см,

принимаемс = 2,5∙h₀ = 2,5∙27 = 67.5 см

Изм.

Лист

№ докум.

Подпись

Дата

Лист

Другое условие при Q = Q_max – q₁∙c = 53,55∙10³ – 115,23∙67,5 = 45,77∙10³Н и значении = 27,96∙10³> 45,77∙10³Н – не удовлетворяется, следовательно, поперечная арматура требуется по расчёту.

На приопорном участке длиной l/4 устанавливаем в каждом ребре плиты поперечные стержни Ø5 B500 с шагом s=h/2=15см, в средней части пролёта с шагом s=3h/4≈25см.

A_sw=2∙0,196=0,392см²

R_sw=290 МПа

q_sw= 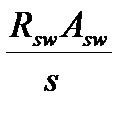= =757,87 Н/см

Влияние свесов сжатых полок:

φ_f=2∙0,75∙3∙h^Ꞌ_f() =2∙0,75∙3∙5∙() =0,3˂0,5

1+φ_n+ φ_f =1+0,37+0,3=1,67>1,5 – принимаем 1,5

Q_bmin = φ_b3(1+φ_n+ φ_f)R_bt∙b∙h_o =0,6∙1,5∙0,9(100)∙14∙27=30,62∙10³ Н

Условиеq_sw =757,87 Н/см> = = 567,04 Н/см – удовлетворяется.

Требование s_max = 25,73см >s=15см – удовлетворяется.

Для расчёта прочности вычислим:

M_b= φ_b2(1+ φ_n+ φ_f)R_bt∙b∙ =2∙1,5∙0.9(100)∙14∙27²=275,56∙10⁴Н∙см

Поскольку q₁ = 115,23 Н/см ˂ 0,56q_sw = 0,56∙757,87 = 424,41 Н/см, вычислим значение с по формуле:

с= 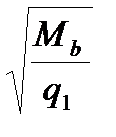= = 154см >3,33h_o= 3,33∙27 = 90см – принимаем с=90см.

Тогда Q_b= Q_bmin = = =30,62∙10³ Н

Поперечная сила в вершине наклонного сечения:

Q = Q_max – q₁∙c = 53,55∙10³ – 115,23∙90 = 43,18∙10³Н

Длина проекции расчётного наклонного сечения:

с_о = 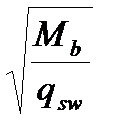= = 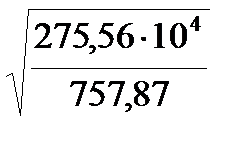60,3см >2h_o= 2∙27 = 54см – принимаем с_о = 54см.

При этом Q_sw = q_swc_o = 757,87∙54 = 40,92∙10³H

Условие прочности:

Q_b+Q_sw = 30,62∙10³+40,92∙10³ = 71,54∙10³H>Q = 43,18∙10³H – прочность

обеспечивается.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

Прочность проверяем по сжатой наклонной полосе:

μ_sw = = =0.0019

α = 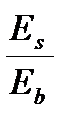= =7,917

φ_ω1 = 1+5α μ_sw= 1+5∙7,92∙0,0019 = 1,075

β = 0,01

φ_b1 = 1 – βR_b = 1 – 0,01∙11,5 = 0,885

Условие прочности:

0,3∙φ_ω1∙φ_b1∙R_b∙b∙h_o = 0,3∙1,075∙0,885∙11,5(100)∙14∙27 = 124,07∙10³H>Q_max = 53,55∙10³ – условие удовлетворяется.