2018-01-21
817
• Для більш простого проектування регуляторів замість частотних характеристик використовують логарифмічні частотні характеристики (наближені методи розрахунків).
• Логарифмічна амплітудна частотна характеристика (ЛАЧХ):
залежність величини 
відlg 
[декада],
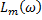=20lgA(ω) [дБ]
• Логарифмічна фазова частотна характеристика (ЛФЧХ):
залежність величини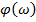 
відlg ,
• Разом ЛАЧХ і ЛФЧХ називаються логарифмічною амплітудно-фазовою частотною характеристикою (ЛАФЧХ) або діаграмою Боде.
• Важливі властивості логарифмічних характеристик
• 1. ЛАЧХ і ЛФЧХ для добутку передавальних функцій обчислюються як суми ЛАЧХ і ЛФЧХ окремих ланок:
• В області високих і низьких частот ЛАЧХ асимптотично наближаються до прямих, нахил яких складає ± 20 дБ / дек (децибел на декаду), ± 40 дБ / дек і т.д.
На низьких частотах:
• Асимптота (ЛАЧХ) має нульовий наклон, якщо W (0) = 1 ≠ 0 (ланка відноситься до класу позиційних ланок, має постійний ненулевий статичний коефіцієнт посилення).
• Якщо W (0) = 0, передавальна функція містить множник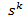 
(k > 0), який відповідає похідній порядку k. У цьому випадку нахил ЛАЧХ на низьких частотах дорівнює k⋅ 20 дБ / дек.
|
|
|
• Якщо W (0) = ∞, ланка містить один або кілька інтеграторів, тобто в знаменнику є співмножник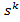 
. Тоді нахил ЛАЧХ на низьких частотах дорівнює - k⋅ 20 дБ / дек.
На високих частотах:
• Нахил ЛАЧХ визначається різницею ступенів чисельника і знаменника передавальної функції. Якщо чисельник має ступінь m, а знаменник - ступінь n, то нахил останньої асимптоти дорівнює 20 (m-n) дБ / дек.
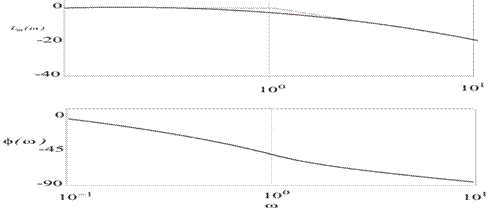
• На малюнку показані точна (суцільна лінія) і асимптотична (штрихова червона лінія) ЛАФЧХ для ланки першого порядку з передавальної функцією W(s)=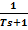 
ЛЕКЦІЯ 4. ЧАСОВІ ХАРАКТЕРИСТИКИ
План лекції
4.1. Перехідна характеристика
4.2. Вагова характеристика
4.3. Усталений режим
4.4. Статична характеристика
