Властивості перетворення Лапласа

 

1. Лінійність .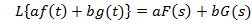

2. Множення на число .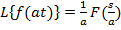

3. Множення зображень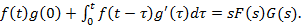

4. Теорема про згортку.Перетворенням Лапласа згортки двох оригіналів є добуток зображень цих оригіналів:

.

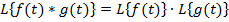Згорткою (англ. convolution) двохфункцій 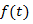та 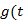)називаютьвираз

)= =

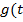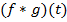5. Диференціювання і інтегрування оригіналу

,

-…- ;

= .

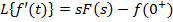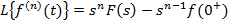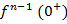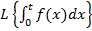6. Дифренціювання та інтегрування зображення

= ,

= .

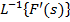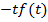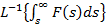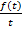7. Запізнення зображень і оригіналів

, ;

,

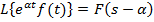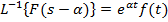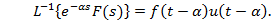
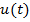- функція Хевісайда.

8. Теорема розкладання. Якщо F(s) = B (s) / A (s) є дрібно-раціональної функцією (A (s), B (s) - поліноми від s) і ступінь полінома чисельника менше полінома знаменника n, то її оригіналом є функція

,

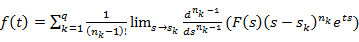де 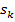- корені рівняння A (s), 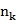- їх кратності і q – числорізних коренів.

Якщо коріння 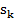прості, то

.

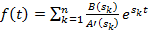Наведені формули справедливі при t 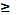0.

При t<0 за визначенням функції-оригіналу x (t) = 0.

 

Приклад 1.

Визначити функцію x(t), зображення якої має вигляд

.

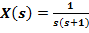Рішення.В даному випадку

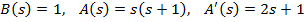
Полюсами функції X(s) єрішення рівняння 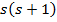=0.

Вони є простими: .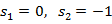

 

Тому згідно з формулою

= = + :

.

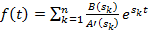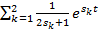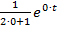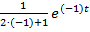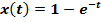Таблиця перетворення Лапласа для деяких функцій

№	Оригинал x(t)	Изображение X (s)

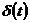
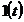
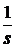
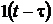
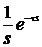
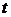
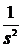
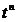
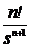
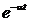
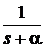
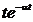
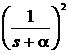
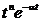
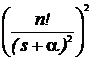
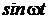
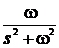
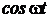
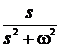
Згідно до математичних перетворень рішення диференційного рівняння

 

 

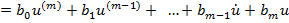
за допомогою перетворень Лапласа дає такий же результат як застосування оператора диференціювання (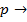 s)

= .

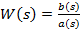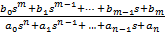Або ,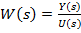

де 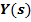та 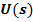- зображення вихідного та вхідного сигналу.

Передавальною функцією системи (ланки) в зображеннях Лапласа називають відношення зображень її вихідної і вхідної змінних при нульових початкових умовах, яке має найменший порядок:

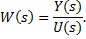
Згідно з визначенням передавальна функція в зображеннях Лапласа не може мати рівні між собою нулі та полюси, так як в цьому випадку її порядок можна було б знизити, скоротивши чисельник і знаменник на спільний дільник.

Якщо система (ланка) має кілька входів, то при визначенні передавальної функції щодо певної вхідної змінної інші вхідні змінні вважають рівними нулю.

Якщо відомі передавальна функція об’єкту і зображення вхідного впливу, то зображення вихідного сигналу

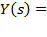W(s)U(s).

Тоді вихідний сигнал як функцію часу можна знайти за допомогою оберненого перетворення Лапласа:

y(t) =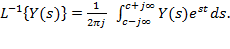

Для цього використовують теорему розкладання.

 

Приклад 2.

Визначити передавальні функції ланок, описуваних рівняннями:

а) 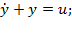б) .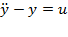

Рішення. У символічній формі ці рівняння записуються у вигляді:

а) 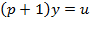; б)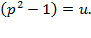

Їх передавальні функції в операторній формі відповідно дорівнюють:

а) 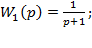б)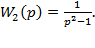

Передавальні функції в зображеннях Лапласа мають вигляд:

а) 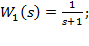б)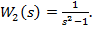

Передатна функція в операторній формі є оператором.

Її не можна розглядати як звичайну дріб. Зокрема, не можна чисельник і знаменник скорочувати на спільний множник, якщо він містить оператор диференціювання.

Приклад 3.

Розглянемо ОК, що описується рівнянням 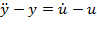. В операторній формі: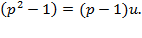

Тоді передавальна функція в операторній формі:

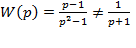або .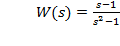

Передавальна функція в зображеннях Лапласа не може служити описом ОК при довільних початкових умовах, бо його передавальна функція в операторній формі має рівні між собою нулі і полюси: р=1.

 

 

 

ЛЕКЦІЯ3. ЧАСТОТНІХАРАКТЕРИСТИКИ

План лекції

3.1. Частотна передавальна функція

3.2. Амплітудна та фазова частотні характеристики

3.3. Логарифмічні частотні характеристики