| Розглянемо багатоканальну систему з незалежними (автономними) каналами. Система описується m операторними рівняннями | |

| (4.9)




|
| y – вектор виходу (вихідних змінних) | u – вектор керувань (вхідних керуючих дій) |
• 
• 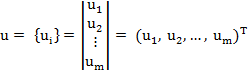
•  (p),
(p),  (p) - елементи відповідних матриць А, В.
(p) - елементи відповідних матриць А, В.
Cистема (4.9) у матричній формі:
• 
або 𝐴(𝑝)𝑦= 𝐵(𝑝)𝑢. (4.10)
•  запишемо у вигляді
запишемо у вигляді 
та отримаємо передавальну функцію багатоканальної системи з незалежними каналами:


| Багатоканальну систему з перехресними зв’язками розглянемо на прикладі двоканальної системи: | |

|


 - передавальні функції основних каналів системи, - передавальні функції основних каналів системи,
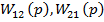 - передавальні функції перехресних зв’язків. - передавальні функції перехресних зв’язків.
|
• У загальному випадку:





Моделі ВВ збурених систем
| Збурення 𝒇(𝒕), що діє на об’єкт, розглядається як додатковий вхідний сигнал | Модель лінійної одноканальної системи із збуреннями | |
 
| 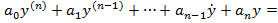
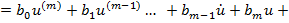

| |

|
 , ,

| |

|

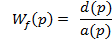
| |
 передавальна функція за збурюючою дією, передавальна функція за збурюючою дією,
 - передавальна функція за керуючою дією. - передавальна функція за керуючою дією.
| ||
Лекція 5. Операційний метод опису лінійних САК
• 5.1. Перетворення Лапласа та його основні властивості.
• 5.2. Передавальна функція.
 2018-01-21
2018-01-21 630
630








