В лекції 4 розглядалася модель одноканальної САК (4.1):

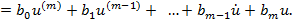
Застосовуючи оператор диференціювання була отримана передавальна функцієя в операторній формі (4.8):
 =
=  або
або
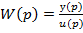 .
.
• Для знаходження розв’язку неоднорідного рівняння застосовують перетворення Лапласа.
• Перетворення Лапла́са — інтегральне перетворення, що зв'язує функцію комплексної змінної (зображення) F(s) з функцією дійсної змінної (оригінал) f(t).
• Пряме перетворення:
F(s) = L 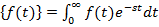 . (5.1)
. (5.1)
• Зворотне перетворення:
f(t) = 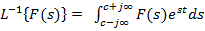 . (5.2)
. (5.2)
F(s) - зображення функції f(t) за Лапласом або просто зображення, s=σ+jω.
f(t) - оригінал функції.
 - оператор Лапласа,
- оператор Лапласа,  - зворотний оператор Лапласа.
- зворотний оператор Лапласа.
Передбачається, що функція f(t), що піддається перетворенню Лапласа, має такі властивості:
• 1) функція f(t) визначена і кусково-дифференцируєма на інтервалі [0, ∞);
• 2) f(t) = 0 при t < 0;
• 3) існують такі позитивні числа с і М, що 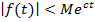 при
при 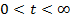 .
.
З допомогою перетворення Лапласа досліджуються властивості динамічних систем і розв'язуються диференціальні і інтегральні рівняння
Властивості перетворення Лапласа
1. Лінійність 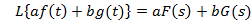 .
.
2. Множення на число  .
.
3. Множення зображень 
4. Теорема про згортку. Перетворенням Лапласа згортки двох оригіналів є добуток зображень цих оригіналів:
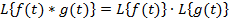 .
.
Згорткою (англ. convolution) двохфункцій  та
та  ) називаютьвираз
) називаютьвираз  )=
)=  =
= 
Диференціювання і інтегрування оригіналу
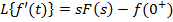 ,
,
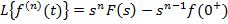 -…-
-…- 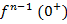 ;
;
 =
=  .
.
 2018-01-21
2018-01-21 1411
1411








