Критерій стійкості Рауса

Умовастійкості лінійноїсистеми виражаєтьсяутім, щовсікореніхарактеристичногорівняння повиннірозташовуватисявлівійпівплощинікомплексноїзмінної.

• Модель системи (ВВ):

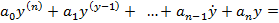
• Характеристичне рівняння: 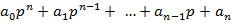=0

• (Або

• Алгебраїчні критерії стійкості дозволяють судити про стійкість системи за коефіцієнтами характеристичного рівняння.

• Критерій стійкості Рауса.

• Цей критерій стійкості був у 1877 р. запропонований англійським математиком Э. Раусом у вигляді деякого правила (алгоритму), який найбільш просто пояснюється наведеною таблицею.

• У першому рядку таблиці записують у порядку убування індексів коефіцієнти характеристичного рівняння, що мають парний індекс: ; у другому рядку – коефіцієнти з непарним індексом: . Любий з інших коефіцієнтів таблиці визначають як

,

де ;

k - індекс, що означає номер стовпця таблиці; i – індекс, що означає номер рядка таблиці.

• Зазначимо, що число рядків таблиці Рауса дорівнює степені характеристичного рівняння плюс одиниця. Після того як таблиця Рауса заповнена, по ній можна судити про стійкість системи.

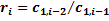
Коефіцієнт	рядок (i)	Стовпець (k)
			…
					…
					…
					…
					…
	…	…	…	…	…
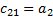
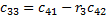
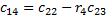
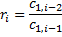
	i				…
	…	…	…	…	…

n -парне.

Для того щоби система автоматичного регулювання була стійка, необхідно і достатньо, щоби коефіцієнти першого стовпця таблиці Рауса мали однакові знаки, тобто для 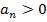були додатними: , , …

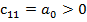• Приклад.

Дослідити стійкість системи за допомогою критерія Рауса: ,

Визначимо передаточну функцію замкнутої системи:

.

Характеристичний многочлен системи A(p)=

• Складемо таблицю Рауса:

Коефіцієнт	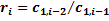Pядок (i)	Стовбчик (k)
-
-

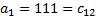
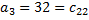
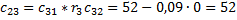
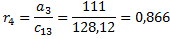
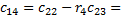
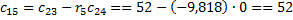
• Є дві зміни знака коефіцієнтів першого стовбчика, отже, система нестійка, а характеристичне рівняння має два правих корня.