Основнаумовастійкості

ТЕОРІЯ АВТОМАТИЧНОГО КЕРУВАННЯ

Лекції

Змістові модулі 3,4

Лекція 12. Стійкість САК

12.1. Поняття стійкості лінійних систем.

12.2. Види стійкості.

12.3. Основна умова стійкості.

12.4. Необхідна умова стійкості.

Поняття стійкості лінійних систем

Стійкість систем автоматичного керування є однією з найважливіших умов її працездатності, тому що стійкість містить у собі вимогу загасання перехідних процесів у часі.

 

Будемо розглядати стійкість лінійних (лінеаризованих) систем.

 

Під стійкістю системи розуміється здатність її повертатися до стану сталої рівноваги після зняття збурення, що порушило цю рівновагу. Нестійка система безперервно віддаляється від рівноважного стану або здійснює навколо нього коливання із зростаючою амплітудою.

 

Стійкість системи автоматичного керування (САК) - здатність САК нормально функціонувати і протистояти різним неминучим збуренням (впливам). Стан САК називається стійким, якщо відхилення від нього залишається як завгодно малим при будь-яких досить малих змінах вхідних сигналів.

 

Стійкість лінійної системи визначається не характером обурення, а структурою самої системи. Кажуть, що система стійка "в малому", якщо визначений факт наявності стійкості, але не визначені її межі. Система стійка "у великому", коли визначені межі стійкості і те, що реальні відхилення не виходять за ці межі.

 

Під стійкістю лінійної системи розуміють властивість загасання перехідного процесу з часом, інакше кажучи, – наступна властивість власного (вільного) руху системи: при

 

• 1. Стійкість «вхід-вихід»

• Зазвичай для інженерів-практиків в першу чергу важливо, щоб система не «пішла в рознос», тобто, щоб керована величина не росла необмежено при всіх допустимих вхідних сигналах. Якщо це так, кажуть, що система має стійкість «вхід-вихід», тобто при обмеженому вході вихід також обмежений. Зауважимо, що при цьому нас не цікавить, як змінюються внутрішні змінні об'єкта, важливий тільки вхід і вихід.

• Розглянемо ванну, яка наповнюється водою з крана. Модель цієї системи - інтегруюча ланка. При постійному (обмеженому за величиною) вхідному потоці рівень води у ванні буде необмежено збільшуватися (поки вода не поллється через край), тому така системі не володіє стійкістю «вхід-вихід».

 

Види стійкості

• 2. «Технічна» стійкість

• На відміну від стійкості «вхід-вихід», поняття «технічна стійкість» відноситься до автономної системи, у якій всі вхідні сигнали дорівнюють нулю.

 

• Положенням рівноваги називають стан системи, яка знаходиться у спокої, тобто, сигнал виходу y(t) - постійна величина, і всі його похідні дорівнюють нулю. Систему виводять з положення рівноваги і прибирають всі збурення. Якщо при цьому з плином часу (при t → ∞) система повертається в положення рівноваги, вона називається стійкою. Якщо вихідна координата залишається обмеженою (не йде в нескінченність), система називається нейтрально стійкою, а якщо вихід стає нескінченним – нестійкою

 

• Якщо повернутися до прикладу з ванною, стає зрозуміло, що ця система - нейтрально стійка, тому що рівень води залишається постійним, коли ми перекриємо кран. З одного боку, рівень води не повертається до попереднього значення, а з іншого - не зростає нескінченно (система не є нестійкою).

 

• 3. Внутрішнястійкість (математичнастійкість)

• БільшдосконалівизначеннястійкостібуливведеніА. М. Ляпуновим

 

• Система (рівноважнийстанх* = 0) називаєтьсястійкоюзаЛяпуновим, якщодлябудь-якогоε>0 знайдетьсяδ (ε)> 0 таке, щодлявсіхпочатковихзначень зобласті <δідлябудь-якихt> 0 виконуєтьсяумова | x (t, ) | <ε.

• Якщокрімтоговекторстанупрагнедоположеннярівноваги, тобто, (x (t) - x *)→ 0 при t →∞, тосистема. називаєтьсяасимптотичностійкоювположеннірівноваги x*.

 

• Очевидно, щоасимптотичнастійкість - більшсильневимога. Положеннярівноваги, якістійкізаЛяпуновим, аленеасимптотичностійкі, інодіназиваютьсянейтральностійкими (маятникбезтертя, ванназводою).

 

• Положення рівноваги нестійке, якщо для нього не виконується умова стійкості Ляпунова. Це означає, що існує таке ε> 0, що траєкторія x (t) виходить за межі області x(t)-x* <ε при як завгодно малому відхиленні початкового стану від положення рівноваги x*. Наприклад, система переходить в інше положення рівноваги, або x(t) необмежено зростає.

 

• Говорячи про внутрішню стійкості, розглядають не тільки вихід, але і всі змінні, які описують стан системи

 

 

• В математичній теорії систем вектор стану позначають через x(t), а рівняння руху системи записують у вигляді (модель ВСВ):

 

• Стійкість означає, що всі рухи x(t), які починаються близько від положення рівноваги x *, при всіх t залишаються в деякій околиці x*. Краще, якщо система не просто стійка, а ще й повертається в положення рівноваги, тобто, x(t) прагне до x* при t → ∞ (асимптотична стійкість).

• На малюнку показані рухи стійкої (1), асимптотично стійкої (2) і нестійкої (3) систем. Для простоти передбачається, що положення рівноваги x * - це початок координат.

• Стійкість визначається для деякого положення рівноваги. Для нелінійної системи може бути кілька положень рівноваги, причому деякі з них можуть бути стійкі, а деякі - ні. В положенні рівноваги всі похідні дорівнюють нулю.

 

 

Технічна стійкість	Математична стійкість
Система нейтральна	Система стійка за Ляпуновим
Система стійка	Система асимптотично стійка
Система нестійка	Система нестійка

Основнаумовастійкості

Будемо вважати, що система описується диференціальним рівнянням (y – вихідна змінна, u – керуюча змінна, f – збурення):

(12.1)

В операторній формі:

(12.2)

 

Загальне рішення рівняння (12.1) має вигляд

(12.3)

де - частинне рішення рівняння (12.1), - загальне рішення відповідного однорідного рівняння.

Загальне рішення однорідного рівняння описує вільний рух системи управління (тобто рух за відсутності зовнішних впливів), який визначається тільки початковими умовами.

Частинне рішення описує вимушений рух, обумовлений зовнішніми впливами.

• Характеристичне рівняння для (12.1) має вигляд

(12.3)

якщо вважати, що р - довільна змінна.

Корені характеристичного рівняння дозволяють знайти , тобто визначають вільний рух системи:

.

Для n=2: 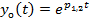. (12.4)

• Характеристичне рівняння – це алгебраїчне рівняння, яке відповідає однорідному диференційному рівнянню. Його можна одержати шляхом використання підстановки Ейлера в однорідне диференційне рівняння.

• Якщо відома передавальна функція, то характеристичне рівняння можна отримати прирівнявши характеристичний поліном (знаменник дробу) нулю.

Розглянемо окремо можливі значення коренів і одержимо умову стійкості САК.

 

1. Нехай корінь рівняння (12.3) – дійсне число. Позначимо його літерою а.

1-й випадок а < 0.

Якщо а < 0, то можна записати, що: а = – |a|. Підставимо в (12.4), і матимемо розв’язок однорідного рівняння у вигляді:

 

З бігом часу t → ∞ розв’язок рівняння спадає до нуля. Графік його показано на рисунку. Це свідчить, що система прагне до певного сталого стану, тобто система стійка.

 

 

• 2-й випадок а 0.

 

Якщо: а < 0, то: а = |a|. Підставимо в (12.4), і матимемо розв’язок однорідного рівняння у вигляді:

.

З бігом часу t → ∞ розв’язок рівняння збільшується.

Графік функції, яка відповідає розв’язку рівняння показано на рисунку. З часом значення величин y(t) зростає до нескінченності. Це свідчить, що система є нестійкою.

 

 

• 3-й випадок

 

Підставимо в (12.4), і матимемо: .

Вихідна величина залишається постійною. Графік розв’язку рівняння показано на рисунку. Тут ми маємо систему на межі стійкості.

 

• Висновок:

У випадку дійсного кореня, коли корінь рівняння менше нуля, система є стійкою, коли корінь дорівнює нулю – система знаходиться на межі стійкості, а коли корінь більше нуля – система нестійка

 

• 2. Нехай корінь характеристичного рівняння (12.3) – комплексне число.

Комплексні корені завжди є комплексно спряженими. Позначимо ці корені так:

Тоді розв’язки однорідного рівняння матимуть вигляд:

 

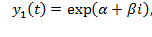
З математики відомо, що коли – є розв’язком рівняння, то і їх сума також буде розв’язком цього рівняння:

 

 

або після деяких перетворень:

 

• Розв’язком рівняння є функція, яка має два множники: перший - це експонента аналогічна, як і в випадку дійсного кореня, другий – гармонічна функція cos(βt). Ми маємо періодичні коливання cos(βt), амплітуда яких змінюється за законом .

• Якщо α< 0, то амплітуда коливань з часом зменшується, якщо α>0, то вона збільшується і при α=0 – лишається постійною.

 

 

• Основна умова стійкості: