2018-01-21
464
Переносе осей.
Пусть 
- центральные оси для данной фигуры, а
и 
- произвольные оси параллельные осям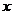 
и 
.
Найдем моменты инерции для осей и , через, как выражаются, “старые” моменты инерции относительно осе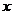й и .
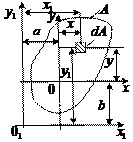Связь между “новыми” и “старыми” координатами произвольной элементарной площадки будут выглядеть
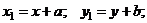
где 
и 
- координаты старого центра в новых осях. Подставляя эти выражения в формулы для моментов инерции, и учитывая, что оси - центральные получаем:
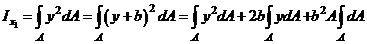
Проделывая аналогичные выкладки и для других моментов, получаем следующий закон преобразования моментов:
; 
; 
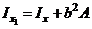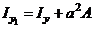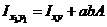
Первыми двум выражениям можно придать словесную формулировку: момент инерции относительно какой-либо оси равняется моменту относительно оси центральной параллельной данной плюс площадь на квадрат расстояния между осями.
