Моменты инерции простейших фигур

а) Момент инерции для прямоугольника относительно центральной оси:

б) Треугольник

Момент инерции относительно оси :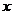

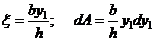
Используя формулу преобразования момента инерции при параллельном переносе осей, получаем выражение для центрального момента инерции:

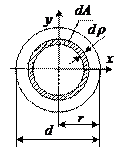в) Круг

Из соображений симметрии заключаем, что все центральные оси обладают равными моментами инерции. Поэтому 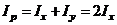Найдем вначале полярный момент инерции: или через диаметр:

г) Кольцевое сечение.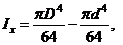

обозначив 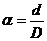, имеем