Напряжения при косом изгибе

В силу высказанных ранее причин мы не будем интересоваться касательными напряжениями, возникающими в данном случае. Рассмотрим сечение балки. Ос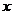и и - главные центральные оси сечения. Плоскость действия изгибающего момента в сечении не совпадает с плоскостями, в которых лежат главные оси.

След плоскости изгибающего момента на плоскости сечения будем называть силовой линией. Угол между силовой линией и положительным направление оси 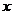обозначим . Пусть точка с координатами 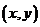- произвольная точка сечения. Наша задача – найти напряжение в данной точке, т.е. установить закон изменения напряжений по сечению: .

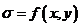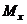Разложим изгибающий момент на два момента и - и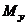згибающие относительно главных центральных осей.

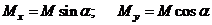
Используя принцип независимости действия сил, определим напряжение, как сумму напряжений от составляющих моментов

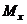и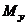

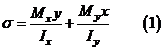
Как видим, косой изгиб представляет собой комбинацию двух прямых изгибов относительно главных осей. Если использовать выражения для 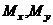, то полученной формуле можно придать другой вид: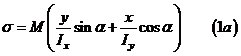

Напряжения в сечении распределяются по линейному закону (если откладывать в каждой точке вектор напряжений, то множество концов векторов будет плоскостью). Нас прежде всего интересует величина наибольшего по модулю напряжения в сечении.

Поступим следующим образом. Вначале найдем нейтральную линию в сечении, т.е. такую линию, в точках которой напряжения равны нулю. Для этого нужно приравнять выражение (1) или (1а) нулю:

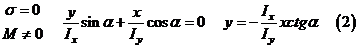
Уравнение (2) однородно, следовательно нейтральная ось проходит через центр тяжести. Можно показать, что нейтральная линия не перпендикулярна к силовой.

На самом деле. Угловой коэффициент нейтральной линии: 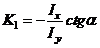, а силовой лини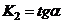и . При ,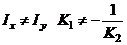

т.е. условие перпендикулярности не выполняется. (Что будет при 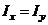?) Нанеся на чертеж сечения, нейтральную линию мы можем убедиться что она отклоняется в сторону более “слабой” оси, т.е. оси с меньшим моментом инерции.

В силу характера распределения напряжений, наибольшие по модулю напряжения возникают в точке наиболее удаленной от нейтральной линии. Пусть такой будет точка 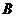с координатами 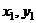(рис.6). Подставив в уравнение для напряжений координаты этой точки, получим выражение для максимальных по модулю напряжений

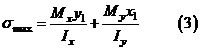Пример.