Изгиб стержня прямоугольного сечения при идеальном

Упруго-пластичном материале.

Пусть материал следует диаграмме идеального упругопластического материала. Связь между напряжениями и деформациями в этом случае выглядит

1) при 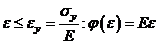(закон Гука)

2) при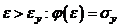

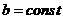
Подставим эти выражения в интеграл (5)

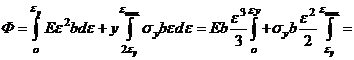
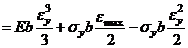
учтем, что 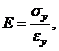тогда 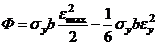подставим в (4)

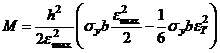
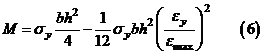
Напомним, что 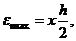тогда (6) можно выразить (учтя также ):

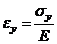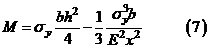
Решим (7) относительно кривизны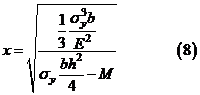

Анализируя (7), мы видим, что наибольшее значение момента не превышает величины: 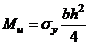, которую назовем предель-

ным моментом. Это значение соответствует полному переходу сечения в пластическое состояние.

Однако, для того чтобы момент достиг предельного значения, как показывает (8) кривизна должна обратиться в бесконечность, что конечно невозможно. Таким образом, величина 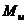в действительности не может быть достигнута.

Величина 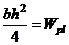называется пластическим моментом сопротивления (сравним с моментом сопротивления ).

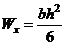Разумеется, что формула (8), выведенная в предположении,

что балка работает в упруго-пластической стадии, неприменима при малых значениях момента, соответствующих упругой работе.

Значение в (8) должно находиться в пределах

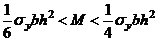
ЛЕКЦИЯ XVII