Выберем основную систему таким образом, чтобы неразрезная балка обратилась в совокупность однопролетных шарнирных опертых балок. Для этого разрежем сечения над опорами и вставим в разрезы шарниры. Т.к. врезав над опорами шарниры, мы устраним связь препятствующую взаимному повороту сечений в шарнире, то, понятно, что основные неизвестные у нас будут являться изгибающими моментами в опорных сечениях – опорными моментами.
Рассмотрим произвольную балку:
Пусть  - номера следующих друг за другом произвольных опор, а
- номера следующих друг за другом произвольных опор, а  и
и  - пролеты, заключенные между данными опорами. Составим каноническое уравнение для
- пролеты, заключенные между данными опорами. Составим каноническое уравнение для 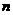 опоры:
опоры:

Нетрудно заметить, что только три коэффициента:  отличны от нуля, а остальные обращаются в нуль.
отличны от нуля, а остальные обращаются в нуль.
Вычислим коэффициенты и свободные члены:



Подставим эти выражения в (1), умножим уравнение на 6 и
обозначим: 
 Полученное уравнение носит название “уравнение трех моментов”,
Полученное уравнение носит название “уравнение трех моментов”, 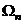 и
и  - площади эпюр моментов в основной системе следует рассматривать как величины алгебраические и приписывать им знак плюс в случае, если моменты положительны, и знак минус в случае отрицательных моментов.
- площади эпюр моментов в основной системе следует рассматривать как величины алгебраические и приписывать им знак плюс в случае, если моменты положительны, и знак минус в случае отрицательных моментов.
 Система канонических уравнений, составленных таким образом, обладает тем преимуществом, что какого бы порядка она не была, каждое из уравнений будет содержать не более 3 неизвестных величин. Т.е. матрица
Система канонических уравнений, составленных таким образом, обладает тем преимуществом, что какого бы порядка она не была, каждое из уравнений будет содержать не более 3 неизвестных величин. Т.е. матрица  будет трехдиагональной (см. рисунок). Ширина полосы равняется 3. Вне этой полосы коэффициенты равны нулю, и они не должны сохраняться в машинной памяти. Задачи, приводимые к подобным матрицам, эффективны для расчетов на ЭВМ, т.к. они требуют меньшей машинной памяти и меньшего времени для расчета.
будет трехдиагональной (см. рисунок). Ширина полосы равняется 3. Вне этой полосы коэффициенты равны нулю, и они не должны сохраняться в машинной памяти. Задачи, приводимые к подобным матрицам, эффективны для расчетов на ЭВМ, т.к. они требуют меньшей машинной памяти и меньшего времени для расчета.
При малой степени статической неопределимости эффективность применения уравнений (2) меньше, но тем не менее и здесь есть удобство, заключающееся в автоматической записи метода сил.
ЛЕКЦИЯ XVI
 2018-01-21
2018-01-21 1581
1581
