2018-01-21
425
В прошлой лекции мы научились находить величину предельного момента для прямоугольного сечения. Найдем величину предельного момента, т.е. момента, соответствующего переходу всего сечения в пластическое состояние для произвольного сечения, имеющего одну ось симметрии (ось 
). Напомним, что в действительности предельный момент не может быть реализован. Пусть материал по разному работает на растяжение и сжатие и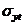 
предел текучести при растяжении, а 
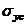- предел текучести при сжатии.
Рассмотрим сечение, полностью перешедшее в пластическое состояние.
Положение нейтральной оси (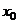
) в предельном состоянии найдем из равенства нулю проекций сил, действующих в сечении на ось балки: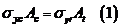 
если материал одинаково работает на растяжение и сжатие, то
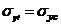и условие выглядит: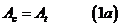 
Предельный момент в сечении равен
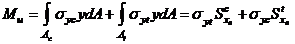, где
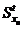и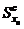 
статические моменты растянутой и сжатой зоны сечения
относительно оси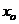 
.
Если материал одинаково работает на растяжение и сжатие, то
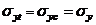
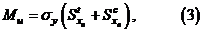
Величину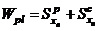 
называется пластическим моментом сопротивления.
|
|
|
Если ось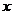 
- ось симметрии, то нейтральная ось совпадает с ней и 
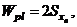где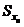 
- статический момент половины сечения относительно нейтральной оси.
Итак!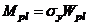 
Когда момент в сечении достигает значения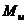 
, то сечение не способно воспринимать возрастающую нагрузку и ведет себя как шарнир, называемый пластическим шарниром. Этот шарнир характерен следующим:
а) Он односторонний и при уменьшении нагрузки закрывается.
б) В нем действуют две противоположно направленные пары с моментами равными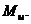 
Введение пластического шарнира означает идеализацию картины распространения пластических деформаций в балке при поперечном изгибе. Пластическая зона распространяется по длине балки (см. предыдущую лек-
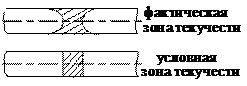цию), а допуская, что в сечении возник пластический шарнир, мы ограничиваем зону текучести одним сечением.
