2018-01-21
859
Рассмотрим стержень, работающий в условиях чистого изгиба. Пусть поперечное сечение стержня имеет две оси симметри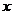и 
и 
.
Будем считать, что материал одинаково работает как на растяжение, так и на сжатие и нам задан закон, связывающий напряжения с деформацией: 
В основу решения положена гипотеза плоских сечений (см. лекция 6). 
или обозначим кривизну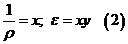 
Форма поперечного сечения балки задается шириной: 
где
вместо аргумента можно ввести безразмерную координату 
и рассматривать функцию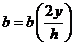 
.
Момент внутренних сил, действующих на элементарную площадку шириной 
и высотой 
(см.рис.) равняется:
Изгибающий момент в сечении (учитывая, что ось 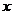-ось симметрии):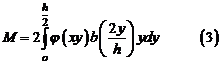 
Выражение (3) можно преобразовать, заменив переменную интегрирования на величину ей пропорциональную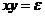 
. Наибольшие деформации возникнут в точке наиболее удаленной от ос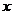и при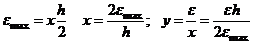 
; 
тогда 
Интеграл 
может быть найден при
простом законе 
и 
аналитически, а в более сложных
случаях численно.
Таким образом, по заданной кривизне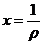 
балки мы можем найти величину изгибающего момента. Задаваясь различными значениями кривизны 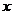, мы можем с помощью (4) найти соответствующие им значения изгибающего момента 
и построить график зависимости от .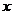
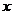Имея этот график, можно по заданному моменту найти величину , затем деформации по формуле 
, а по деформациям из закона 
определить напряжения, возникающие в поперечном сечении балки при заданном моменте.
