В сколько- нибудь сложных случаях, получить критическую силу из решения дифференциального уравнения изогнутой оси сжатого стержня затруднительно.
Поэтому в подобной ситуации проще получить приближенное решение, например, энергетическим методом.
Рассмотрим стержень центрально сжатый силой Р. Условно на рисунке стержень показан шарнирно опертым, но вопрос о граничных
 условиях пока оставим открытым. Пусть сила F меньше эйлеровой критической силы. Если приложить к стержню некоторую поперечную нагрузку Q, то стержень изогнется, но будет находиться в устойчивом равновесном состоянии.
условиях пока оставим открытым. Пусть сила F меньше эйлеровой критической силы. Если приложить к стержню некоторую поперечную нагрузку Q, то стержень изогнется, но будет находиться в устойчивом равновесном состоянии.
Сжимающая сила совершит при этом работу на перемещении 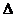 , которое можно найти следующим образом.
, которое можно найти следующим образом.
Укорочение малого элемента длиной  будет равно
будет равно

Учтем, что  , тогда
, тогда 
Потенциальная энергия деформации изогнутого стержня
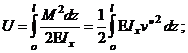 Здесь учтено, что
Здесь учтено, что 
Изменение полной энергии при малом изгибе будет 
Если 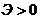 , то стержень устойчив, если же
, то стержень устойчив, если же  ,т.е.
,т.е.  , то сила производит работу большую, чем может накопиться в стержне в виде энергии упругой деформации, избыточная работа идет на сообщение кинетической энергии, стержень приходит в движение и прогибается дальше. Т.е. он неустойчив. Очевидно, что когда сила достигает критического значения, то
, то сила производит работу большую, чем может накопиться в стержне в виде энергии упругой деформации, избыточная работа идет на сообщение кинетической энергии, стержень приходит в движение и прогибается дальше. Т.е. он неустойчив. Очевидно, что когда сила достигает критического значения, то  или
или
 , откуда
, откуда 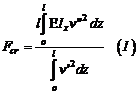
Для получения значения критической силы необходимо задать-
ся формой изогнутой оси. Функцию  надо подбирать таким
надо подбирать таким
образом, чтобы она удовлетворяла граничным условиям. Примеры.
СОДЕРЖАНИЕ
|
 2018-01-21
2018-01-21 1633
1633








