Понятие устойчивости равновесного состояния
деформируемой системы.
Не все теоретически возможные равновесные формы могут быть реализованы в действительности. Реальный объект всегда отличается от расчетной схемы. Всегда имеются неучтенные в расчетной схеме силы, реальная геометрическая форма всегда отклоняется от проектной. Имеются отклонения в свойствах материалов от того, что предусматривалось проектом и т. д. В некоторых случаях эти, казалось бы второстепенные факторы могут привести к тому, что теоретически возможное состояние практически становится неустойчивым.
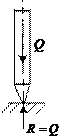 Например, никто не видел следующей картины: идеально прямой карандаш стоит строго вертикально на горизонтальном идеально гладком стекле. В этом случае реакция опорной поверхности направлена строго вертикально и равняется весу карандаша. Две равные по величине действующие по одной прямой и направленные в противоположные стороны силы, должны уравновешиваться, однако данное равновесное состояние реализовать в действительности невозможно. Помимо веса карандаша и реакции поверхности будут действовать и другие силы, например силы обусловленные движением воздуха, карандаш не будут строго прямолинейным, а поверхность стекла совершенно горизонтальной и идеально гладкой и т. д.
Например, никто не видел следующей картины: идеально прямой карандаш стоит строго вертикально на горизонтальном идеально гладком стекле. В этом случае реакция опорной поверхности направлена строго вертикально и равняется весу карандаша. Две равные по величине действующие по одной прямой и направленные в противоположные стороны силы, должны уравновешиваться, однако данное равновесное состояние реализовать в действительности невозможно. Помимо веса карандаша и реакции поверхности будут действовать и другие силы, например силы обусловленные движением воздуха, карандаш не будут строго прямолинейным, а поверхность стекла совершенно горизонтальной и идеально гладкой и т. д.
Будем называть неучтенные силы, отклонения в геометрической форме и т. д., возмущениями.
Определение: будем называть равновесное состояние устойчивым, если оно мало изменяется при малых возмущениях.
Приведем некоторые примеры.
 1. Тяжелый шар на поверхности, имеющий вершины, впадины и горизонтальные участки.
1. Тяжелый шар на поверхности, имеющий вершины, впадины и горизонтальные участки.
В том случае, когда шарик находится на вершине составляющая силы тяжести Т, возникающая при его отклонении, уводит его от первоначального состояния, для шарика, находящегося во впадине сила Т будет возвращать отклоненный шарик в первоначальное состояние и он будет колебаться в окрестности наиболее низкой точки впадины, т. е. при малых отклонениях состояние шарика будет также меняться мало. Случай шарика, находящегося на горизонтальной поверхности, будет случаем, разграничивающим рассмотренные выше неустойчивые и устойчивые равновесные состояния.
Такое состояние называется безразличным
 2. Картину разрушения образца при при растяжении с образованием шейки можно характеризовать, как потерю устойчивости цилиндрической формы образца.
2. Картину разрушения образца при при растяжении с образованием шейки можно характеризовать, как потерю устойчивости цилиндрической формы образца.
По мере приближения состояния образца к точке С цилиндрическая форма образца становится неустойчивой, образуется шейка и малым изменениям силы соответствуют значительные изменения конфигурации системы.
3. Центрально сжатый гибкий стержень
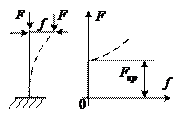 Предполагается, что стержень идеально прямой, а сила приложена строго по оси (что, конечно, практически невозможно). Для того, чтобы судить устойчиво ли данное равновесное состояние, надо приложить горизонтальную возмущающую силу, которая вызовет прогиб. Если сила F невелика, то прогиб окажется малым, равновесное состояние (прямолинейное) практически не изменится.
Предполагается, что стержень идеально прямой, а сила приложена строго по оси (что, конечно, практически невозможно). Для того, чтобы судить устойчиво ли данное равновесное состояние, надо приложить горизонтальную возмущающую силу, которая вызовет прогиб. Если сила F невелика, то прогиб окажется малым, равновесное состояние (прямолинейное) практически не изменится.
Однако, если сила F превысит некоторое значение называющееся критическим 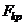 , то равновесное состояние становится неустойчивым, т. е. любые малые возмущения приведут к значительным прогибам. Зависимость между силами и прогибом показана на рисунке. пунктирной линией показано действительное поведение стержня, которое можно обнаружить с помощью нелинейных решений, сплошной чертой показано грубое, линейное решение задачи.
, то равновесное состояние становится неустойчивым, т. е. любые малые возмущения приведут к значительным прогибам. Зависимость между силами и прогибом показана на рисунке. пунктирной линией показано действительное поведение стержня, которое можно обнаружить с помощью нелинейных решений, сплошной чертой показано грубое, линейное решение задачи.
Задача Эйлера
Рассмотрим центрально сжатый шарнирно закрепленный с обоих концов стержень. Необходимо для этого стержня найти критическую силу. Эта задача была решена Эйлером.
Существо задачи состоит в том, что задача об устойчивости по
отношению к заданному возмущению подменяется задачей о возможности существования двух различных форм равновесия при одном и том же значении силы F. Очевидно, что прямолинейная равновесная форма возможна (v = 0).
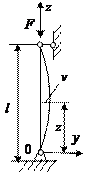 Допустим, что наряду с прямолинейной равновесной формой возможна и криволинейная равновесная форма, показанная на рисунке.
Допустим, что наряду с прямолинейной равновесной формой возможна и криволинейная равновесная форма, показанная на рисунке.
Кривизна стержня на основании закономерности известной из теории изгиба выразится 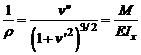
Будем полагать, что угол поворота v ’ – величина малая по сравнению с единицей и тем более мал квадрат этой величины по с равнению с единицей, тогда 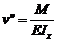
Изгибающий момент в произвольном сечении координатой z  (знак минус увязывает знак прогиба и момента).
(знак минус увязывает знак прогиба и момента).
Дифференциальное уравнение изогнутой оси выглядит
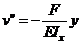 или
или 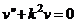 , где
, где 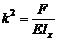 (1)
(1)
Решение этого дифференциального уравнения, как известно

Из граничных условий попробуем найти произвольные постоянные 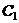 и
и 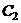
1) при z = l v =0 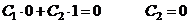
2) при z = 0 v =0 
Возможны две ситуации
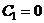 . Откуда v = 0, т.е. получаем прямолинейную равновесную форму
. Откуда v = 0, т.е. получаем прямолинейную равновесную форму 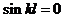
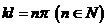
подставим в (1) выражение 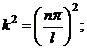
 , откуда
, откуда
найдем выражение силы, при которой помимо прямолинейной равновесной формы, появляется сложная криволинейная равновесная форма
 реальный смысл имеет наименьшее значение силы
реальный смысл имеет наименьшее значение силы
при 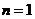 Эйлерова сила – критическая сила
Эйлерова сила – критическая сила 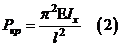
Очевидно, что  - минимальный момент инерции.
- минимальный момент инерции.
Потеря устойчивости будет происходить по синусоиде 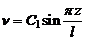 ,
,
Однако, произвольную 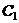 мы так и не смогли найти. Дело в том, что задача о потере устойчивости – задача существенно нелинейна, а мы поступили непоследовательно. С одной стороны мы подошли к задаче как нелинейной, отойдя от принципа начальных размеров, и определив изгибающий момент с учетом изгиба стержня. С другой стороны приняв приближенное выражение для кривизны, мы линеарезовали задачу. Для того чтобы определить прогибы в закретической стадии надо исходить из нелинейного дифференциального уравнения.
мы так и не смогли найти. Дело в том, что задача о потере устойчивости – задача существенно нелинейна, а мы поступили непоследовательно. С одной стороны мы подошли к задаче как нелинейной, отойдя от принципа начальных размеров, и определив изгибающий момент с учетом изгиба стержня. С другой стороны приняв приближенное выражение для кривизны, мы линеарезовали задачу. Для того чтобы определить прогибы в закретической стадии надо исходить из нелинейного дифференциального уравнения.
Однако, главная цель – определение критической силы для стержня нами достигнута.
 2018-01-21
2018-01-21 645
645








