Понятие максимума, минимума, экстремума функции двух переменных аналогичны соответствующим понятиям функции одной переменной.
Пусть функция  определена в некоторой области
определена в некоторой области 

Определение. Точка  называется точкой минимума функции
называется точкой минимума функции  если существует такая d-окрестность точки
если существует такая d-окрестность точки  что для всех точек
что для всех точек  , отличных от
, отличных от  из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство  .
.
Определение. Точка  называется точкой максимума функции
называется точкой максимума функции  если существует такая d-окрестность точки
если существует такая d-окрестность точки  что для всех точек
что для всех точек  , отличных от
, отличных от  из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство  .
.
 Точки минимума и максимума функции
Точки минимума и максимума функции  называются точками экстремума, а значения функции в этих точках – экстремумами функции (минимумом и максимумом соответственно).
называются точками экстремума, а значения функции в этих точках – экстремумами функции (минимумом и максимумом соответственно).
В силу определения точки экстремума функции лежат внутри области определения функции; максимум и минимум имеют локальный характер: значение функции в точке  сравнивается с ее значением в точках, достаточно близких к этой точке. В области определения функции может иметь несколько экстремумов или не иметь ни одного.
сравнивается с ее значением в точках, достаточно близких к этой точке. В области определения функции может иметь несколько экстремумов или не иметь ни одного.
Теорема (необходимое условие экстремума). Если  – точка экстремума дифференцируемой функции
– точка экстремума дифференцируемой функции  , то ее частные производные
, то ее частные производные  в этой точке равны нулю:
в этой точке равны нулю:  .
.
Обратное утверждение справедливо далеко не всегда. Иными словами, если известно, что в некоторой точке  частные производные равны нулю, то это еще не значит, что там есть экстремум. Его там может и не быть.
частные производные равны нулю, то это еще не значит, что там есть экстремум. Его там может и не быть.
Точки, в которых частные производные первого порядка равны нулю, называются критическими или стационарными. В критических точках функция  может иметь экстремум, а может и не иметь.
может иметь экстремум, а может и не иметь.
Теорема 2 (достаточное условие экстремума). Пусть функция  :
:
а) определена в некоторой окрестности критической точки  , в которой
, в которой  и
и  ;
;
б) имеет непрерывные частные производные второго порядка 
Тогда,
если  , то функция
, то функция  в точке
в точке  имеет экстремум:
имеет экстремум:
максимум, если А<0;
минимум, если А>0;
если  , то функция
, то функция  в точке
в точке  экстремума не имеет. В случае
экстремума не имеет. В случае  вопрос о наличии экстремума остается открытым, необходимы дополнительные исследования.
вопрос о наличии экстремума остается открытым, необходимы дополнительные исследования.
Алгоритм исследования функции на экстремум.
1. Найти частные производные первого порядка  и
и  ;
;
2. Решить систему уравнений 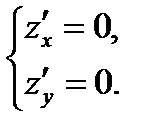 и найти критические точки функции.
и найти критические точки функции.
3. Найти частные производные второго порядка: 
4. Вычислить значения частных производных второго порядка в каждой критической точке и, используя достаточные условия, сделать вывод о наличии экстремума.
5. Найти экстремумы функции.
Пример. Найти экстремумы функции 
Решение.
1. Находим частные производные первого порядка:
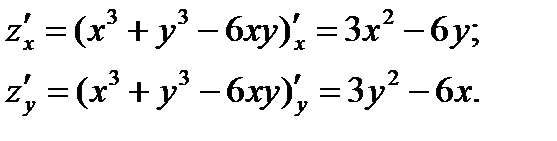
2. Для определения критических точек решаем систему уравнений:
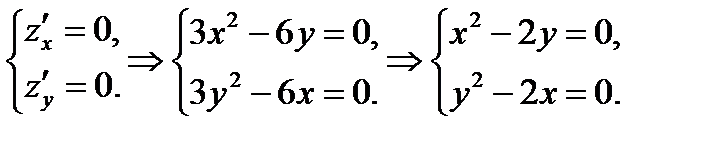
Из первого уравнения системы выразим одну из переменных:  и подставим найденное значение y во второе уравнение, получим:
и подставим найденное значение y во второе уравнение, получим:

Таким образом, имеем две критические точки:  и
и  .
.
3. Вычисляем частные производные второго порядка:

4. Вычисляем значение частных производных второго порядка в каждой критической точке:
Для точки  имеем: имеем:  | Для точки  имеем: имеем:  |
Так как  то в точке то в точке  экстремума нет. экстремума нет. | Так как  то в точке то в точке 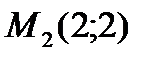 функция имеет минимум. функция имеет минимум. |
5. Находим значение функции в точке 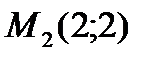 :
:
 .
.
 2017-10-31
2017-10-31 10835
10835
